
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ522 –Η–Ζ 1087 |
 –ù–Α–Ι–¥–Η―²–Β –Ψ―¹―²―Ä―΄–Β ―É–≥–Μ―΄ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α, –Β―¹–Μ–Η –Β–≥–Ψ –≥–Η–Ω–Ψ―²–Β–Ϋ―É–Ζ–Α ―Ä–Α–≤–Ϋ–Α 16, –Α –Ω–Μ–Ψ―â–Α–¥―¨ ―Ä–Α–≤–Ϋ–Α 32√
–ù–Α–Ι–¥–Η―²–Β –Ψ―¹―²―Ä―΄–Β ―É–≥–Μ―΄ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α, –Β―¹–Μ–Η –Β–≥–Ψ –≥–Η–Ω–Ψ―²–Β–Ϋ―É–Ζ–Α ―Ä–Α–≤–Ϋ–Α 16, –Α –Ω–Μ–Ψ―â–Α–¥―¨ ―Ä–Α–≤–Ϋ–Α 32√
–ü―É―¹―²―¨ –Α –Η b -
–Κ–Α―²–Β―²―΄ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α, ―¹ - –≥–Η–Ω–Ψ―²–Β–Ϋ―É–Ζ–Α.
–ü–Μ–Ψ―â–Α–¥―¨
–Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―Ä–Α–≤–Ϋ–Α –Ω–Ψ–Μ–Ψ–≤–Η–Ϋ–Β –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η―è –Κ–Α―²–Β―²–Ψ–≤.
S=ab/2=32√
ab=64√
a=64√
–ü–Ψ
―²–Β–Ψ―Ä–Β–Φ–Β –ü–Η―³–Α–≥–Ψ―Ä–Α:
c2=a2+b2
162=(64√
256b2=642*3+b4
b4-256b2+12288=0
–û–±–Ψ–Ζ–Ϋ–Α―΅–Η–Φ b2=t
t2-256t+12288=0
–†–Β―à–Η–Φ ―ç―²–Ψ
–Κ–≤–Α–¥―Ä–Α―²–Ϋ–Ψ–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β:
D=(-256)2-4*12288=65536-49152=16384
√
t1=(-(-256)+128)/2=192
t2=(-(-256)-128)/2=64
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ –Ψ–±–Α ―¹–Μ―É―΅–Α―è:
1) t=192=b2
b=√
–ü–Ψ
–Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―é, cosα=b/c=8√
α=30¬Α (–Ω–Ψ
―²–Α–±–Μ–Η―Ü–Β)
–ü–Ψ
―²–Β–Ψ―Ä–Β–Φ–Β –Ψ ―¹―É–Φ–Φ–Β ―É–≥–Μ–Ψ–≤ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α, –≤―²–Ψ―Ä–Ψ–Ι –Ψ―¹―²―Ä―΄–Ι ―É–≥–Ψ–Μ ―Ä–Α–≤–Β–Ϋ 180¬Α-90¬Α-30¬Α=60¬Α
2) t=64=b2
b=8
–ü–Ψ
–Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―é, cosα=b/c=8/16=1/2
α=60¬Α (–Ω–Ψ
―²–Α–±–Μ–Η―Ü–Β)
–ü–Ψ
―²–Β–Ψ―Ä–Β–Φ–Β –Ψ ―¹―É–Φ–Φ–Β ―É–≥–Μ–Ψ–≤ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α, –≤―²–Ψ―Ä–Ψ–Ι –Ψ―¹―²―Ä―΄–Ι ―É–≥–Ψ–Μ ―Ä–Α–≤–Β–Ϋ 180¬Α-90¬Α-60¬Α=30¬Α
–û―²–≤–Β―²: 30¬Α –Η 60¬Α
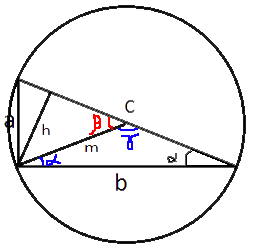 –ü―Ä–Ψ–≤–Β–¥–Β–Φ –Η–Ζ –Ω―Ä―è–Φ–Ψ–≥–Ψ ―É–≥–Μ–Α –Φ–Β–¥–Η–Α–Ϋ―É –Η –≤―΄―¹–Ψ―²―É, –Ψ–±–Ψ–Ζ–Ϋ–Α―΅–Η–≤ –Η―Ö m –Η h ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ.
–ü―Ä–Ψ–≤–Β–¥–Β–Φ –Η–Ζ –Ω―Ä―è–Φ–Ψ–≥–Ψ ―É–≥–Μ–Α –Φ–Β–¥–Η–Α–Ϋ―É –Η –≤―΄―¹–Ψ―²―É, –Ψ–±–Ψ–Ζ–Ϋ–Α―΅–Η–≤ –Η―Ö m –Η h ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ.–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
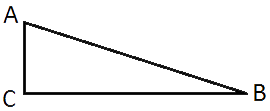
 –£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC ―É–≥–Ψ–Μ C ―Ä–Α–≤–Β–Ϋ 90¬Α, BC=5, AC=3.
–£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC ―É–≥–Ψ–Μ C ―Ä–Α–≤–Β–Ϋ 90¬Α, BC=5, AC=3.
–ù–Α–Ι–¥–Η―²–Β tgB.
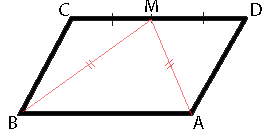 –£ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Β ABCD ―²–Ψ―΅–Κ–Α M βÄî ―¹–Β―Ä–Β–¥–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ CD. –‰–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ MA=MB. –î–Ψ–Κ–Α–Ε–Η―²–Β, ―΅―²–Ψ –¥–Α–Ϋ–Ϋ―΄–Ι –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ βÄî –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ.
–£ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Β ABCD ―²–Ψ―΅–Κ–Α M βÄî ―¹–Β―Ä–Β–¥–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ CD. –‰–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ MA=MB. –î–Ψ–Κ–Α–Ε–Η―²–Β, ―΅―²–Ψ –¥–Α–Ϋ–Ϋ―΄–Ι –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ βÄî –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ.
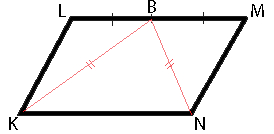 –£ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Β KLMN ―²–Ψ―΅–Κ–Α B βÄî ―¹–Β―Ä–Β–¥–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ LM. –‰–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ BK=BN. –î–Ψ–Κ–Α–Ε–Η―²–Β, ―΅―²–Ψ –¥–Α–Ϋ–Ϋ―΄–Ι –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ βÄî –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ.
–£ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Β KLMN ―²–Ψ―΅–Κ–Α B βÄî ―¹–Β―Ä–Β–¥–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ LM. –‰–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ BK=BN. –î–Ψ–Κ–Α–Ε–Η―²–Β, ―΅―²–Ψ –¥–Α–Ϋ–Ϋ―΄–Ι –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ βÄî –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ.
 –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α, –Β―¹–Μ–Η –Β–≥–Ψ –Κ–Α―²–Β―² –Η –≥–Η–Ω–Ψ―²–Β–Ϋ―É–Ζ–Α ―Ä–Α–≤–Ϋ―΄ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ 40 –Η 85.
–ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α, –Β―¹–Μ–Η –Β–≥–Ψ –Κ–Α―²–Β―² –Η –≥–Η–Ω–Ψ―²–Β–Ϋ―É–Ζ–Α ―Ä–Α–≤–Ϋ―΄ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ 40 –Η 85.
–ö–Α–Κ–Ψ–Ι ―É–≥–Ψ–Μ (–≤ –≥―Ä–Α–¥―É―¹–Α―Ö) –Ψ–Ω–Η―¹―΄–≤–Α–Β―² ―΅–Α―¹–Ψ–≤–Α―è ―¹―²―Ä–Β–Μ–Κ–Α –Ζ–Α 2 ―΅–Α―¹–Α 2 –Φ–Η–Ϋ―É―²―΄?


–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η:
(2023-05-15 11:36:55) –ê–Μ–Β–Κ―¹: –ù–Α–Ι–¥–Η―²–Β –Ψ―¹―²―Ä―΄–Β ―É–≥–Μ―΄ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α, –Β―¹–Μ–Η –Β–≥–Ψ –≥–Η–Ω–Ψ―²–Β–Ϋ―É–Ζ–Α ―Ä–Α–≤–Ϋ–Α 36,–Α –Β–≥–Ψ –Ω–Μ–Ψ―â–Α–¥―¨ ―Ä–Α–≤–Ϋ–Α 162 –Κ–Ψ―Ä–Ϋ―è –Η–Ζ 3
(2023-05-15 11:36:10) –ê–Μ–Β–Κ―¹ : –ù–Α–Ι–¥–Η―²–Β –Ψ―¹―²―Ä―΄–Β ―É–≥–Μ―΄ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α, –Β―¹–Μ–Η –Β–≥–Ψ –≥–Η–Ω–Ψ―²–Β–Ϋ―É–Ζ–Α ―Ä–Α–≤–Ϋ–Α 36,–Α –Β–≥–Ψ –Ω–Μ–Ψ―â–Α–¥―¨ ―Ä–Α–≤–Ϋ–Α 162 –Κ–Ψ―Ä–Ϋ―è –Η–Ζ 3