
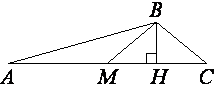 В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=216, HC=54 и ∠ACB=40°. Найдите угол AMB. Ответ дайте в градусах.
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=216, HC=54 и ∠ACB=40°. Найдите угол AMB. Ответ дайте в градусах.
Так как BM -
медиана, значит AM=MC=AC/2=216/2=108
Рассмотрим треугольник MBC.
MH=MC-HC=108-54=54, т.е. получается, что MH=HC.
BH для этого треугольника получается не только
высота, но и
медиана. Это
свойство
равнобедренного треугольника.
По
свойству равнобедренного треугольника: ∠BMC=∠ACB=40°.
∠AMB=180°-∠BMC=180°-40°=140° (т.к. он
смежный)
Ответ: ∠AMB=140°
Поделитесь решением
Присоединяйтесь к нам...
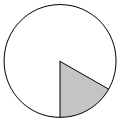 Площадь круга равна 78. Найдите площадь сектора этого круга, центральный угол которого равен 60°.
Площадь круга равна 78. Найдите площадь сектора этого круга, центральный угол которого равен 60°.
 Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=71° и ∠OAB=39°. Найдите угол BCO. Ответ дайте в градусах.
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=71° и ∠OAB=39°. Найдите угол BCO. Ответ дайте в градусах.
 Площадь прямоугольного треугольника равна 128√
Площадь прямоугольного треугольника равна 128√
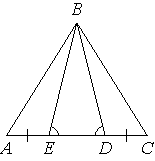 На стороне АС треугольника АВС выбраны точки D и E так, что углы АDB и BEC равны (см. рисунок). Оказалось, что отрезки AЕ и CD тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что углы АDB и BEC равны (см. рисунок). Оказалось, что отрезки AЕ и CD тоже равны. Докажите, что треугольник АВС — равнобедренный.
 Площадь параллелограмма ABCD равна 176. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
Площадь параллелограмма ABCD равна 176. Точка E — середина стороны AD. Найдите площадь трапеции AECB.


Комментарии:
(2015-04-15 16:12:02) Администратор: Ольга.olg1851@yandex.ru, напишите, пожалуйста номер задачи (на fipi.ru) и страницу, что бы эту задачу можно было найти.
(2015-04-15 12:38:00) Администратор: Ольга.olg1851@yandex.ru, напишите, пожалуйста номер задачи (на fipi.ru) и страницу, что бы эту задачу можно было найти.
(2015-04-15 12:36:11) Администратор: Ольга, спасибо за найденную опечатку, исправлено.
(2015-04-15 10:59:55) Ольга.olg1851@yandex.ru: задачу решите пожалуйста. На стороне АВ треугольника АВС взята точка D так, что окружность, проходящая через точки А,С и D, касается прямой ВС. Найти АD, если АС=15, ВС=18 и СD= 10. Поиск по славам ничего не дал, хотя задача ФИПИ математика ОГЭ 2015. Спасибо
(2015-04-15 10:52:50) Ольга: исправьте ошибку в решении 374 МС = НС? МН=НС