Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 39°. Найдите величину угла OMK. Ответ дайте в градусах.
OK перпендикулярен к
касательной (по
свойству касательной), т.е. угол между OK и
касательной равен 90°.
Следовательно, /OKM=90°-39°=51°
Треугольник OMK -
равнобедренный (т.к. OM и OK - радиусы окружности и, соответственно, равны друг другу).
По
свойству равнобедренного треугольника /OKM=/OMK=51°
Ответ: /OMK=51°
Поделитесь решением
Присоединяйтесь к нам...
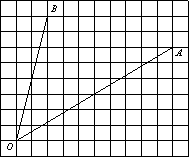Найдите тангенс угла AOB.
В треугольнике ABC DE – средняя линия. Площадь треугольника CDE равна 35. Найдите площадь треугольника ABC.
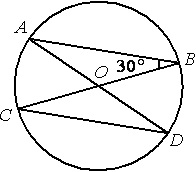В окружности с центром в точке О проведены диаметры AD и BC, угол
ABO равен 30°. Найдите величину угла ODC.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=60°. Найдите угол NMB. Ответ дайте в градусах.
В окружности с центром в точке O проведены диаметры AD и BC, угол OAB равен 70°. Найдите величину угла OCD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: