В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=79 и BC=BM. Найдите AH.
Так как BM -
медиана, значит AM=MC=AC/2=79/2=39,5
Рассмотрим треугольник MBC.
Т.к. BC=BM (по условию задачи), значит этот треугольник
равнобедренный, BH -
высота этого треугольника. По
третьему свойству равнобедренного треугольника MH=HC=MC/2=39,5/2=19,75
Искомая AH=AC-HC=79-19,75=59,25
Ответ: AH=59,25
Поделитесь решением
Присоединяйтесь к нам...
Сторона ромба равна 8, а расстояние от центра ромба до неё равно 2. Найдите площадь ромба.
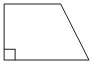Один из углов прямоугольной трапеции равен 121°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
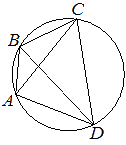Четырёхугольник ABCD вписан в окружность. Угол ABC равен 138°, угол CAD равен 83°. Найдите угол ABD. Ответ дайте в градусах.
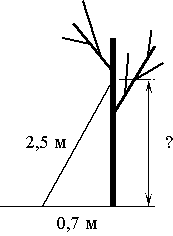Лестницу длиной 2,5 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 0,7 м?
Проектор полностью освещает экран A высотой 100 см, расположенный на расстоянии 170 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 340 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: