
 –ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į
–ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į–ó–į–ī–į—á–į ‚ĄĖ486 –ł–∑ 1087 |
 –ü–Ľ–ĺ—Č–į–ī—Ć –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ä–į–≤–Ĺ–į 32√
–ü–Ľ–ĺ—Č–į–ī—Ć –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ä–į–≤–Ĺ–į 32√
–ü–Ľ–ĺ—Č–į–ī—Ć
–Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ä–į–≤–Ĺ–į –Ņ–ĺ–Ľ–ĺ–≤–ł–Ĺ–Ķ –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł—Ź –ļ–į—ā–Ķ—ā–ĺ–≤:
S=AC*BC/2=32√
–ü—É—Ā—ā—Ć 60-–ł –≥—Ä–į–ī—É—Ā–į–ľ —Ä–į–≤–Ķ–Ĺ —É–≥–ĺ–Ľ BAC.
–ö–ĺ—ā–į–Ĺ–≥–Ķ–Ĺ—Ā BAC:
ctd∠BAC=ctg60¬į=AC/BC=√
AC=BC√
S=AC*BC/2=32√
AC*BC=64√
BC*BC√
BC2=64
BC=8
–ě—ā–≤–Ķ—ā: 8
–ü–ĺ–ī–Ķ–Ľ–ł—ā–Ķ—Ā—Ć —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ–ľ
–ü—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ—Ź–Ļ—ā–Ķ—Ā—Ć –ļ –Ĺ–į–ľ...
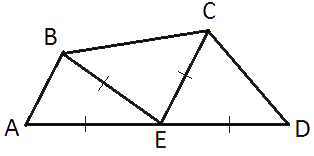 –°–Ķ—Ä–Ķ–ī–ł–Ĺ–į E —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AD –≤—č–Ņ—É–ļ–Ľ–ĺ–≥–ĺ —á–Ķ—ā—č—Ä–Ķ—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ä–į–≤–Ĺ–ĺ—É–ī–į–Ľ–Ķ–Ĺ–į –ĺ—ā –≤—Ā–Ķ—Ö –Ķ–≥–ĺ –≤–Ķ—Ä—ą–ł–Ĺ. –Ě–į–Ļ–ī–ł—ā–Ķ AD, –Ķ—Ā–Ľ–ł BC=8, –į —É–≥–Ľ—č B –ł C —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ä–į–≤–Ĺ—č —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ 92¬į –ł 148¬į.
–°–Ķ—Ä–Ķ–ī–ł–Ĺ–į E —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AD –≤—č–Ņ—É–ļ–Ľ–ĺ–≥–ĺ —á–Ķ—ā—č—Ä–Ķ—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ä–į–≤–Ĺ–ĺ—É–ī–į–Ľ–Ķ–Ĺ–į –ĺ—ā –≤—Ā–Ķ—Ö –Ķ–≥–ĺ –≤–Ķ—Ä—ą–ł–Ĺ. –Ě–į–Ļ–ī–ł—ā–Ķ AD, –Ķ—Ā–Ľ–ł BC=8, –į —É–≥–Ľ—č B –ł C —á–Ķ—ā—č—Ä—Ď—Ö—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ä–į–≤–Ĺ—č —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ 92¬į –ł 148¬į.
 –°—ā–ĺ—Ä–ĺ–Ĺ–į –ļ–≤–į–ī—Ä–į—ā–į —Ä–į–≤–Ĺ–į 40√2. –Ě–į–Ļ–ī–ł—ā–Ķ —Ä–į–ī–ł—É—Ā –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, –ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –ĺ–ļ–ĺ–Ľ–ĺ —ć—ā–ĺ–≥–ĺ –ļ–≤–į–ī—Ä–į—ā–į.
–°—ā–ĺ—Ä–ĺ–Ĺ–į –ļ–≤–į–ī—Ä–į—ā–į —Ä–į–≤–Ĺ–į 40√2. –Ě–į–Ļ–ī–ł—ā–Ķ —Ä–į–ī–ł—É—Ā –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, –ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –ĺ–ļ–ĺ–Ľ–ĺ —ć—ā–ĺ–≥–ĺ –ļ–≤–į–ī—Ä–į—ā–į.
 –í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC –Ī–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–į BE –ł –ľ–Ķ–ī–ł–į–Ĺ–į AD –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ—č –ł –ł–ľ–Ķ—é—ā –ĺ–ī–ł–Ĺ–į–ļ–ĺ–≤—É—é –ī–Ľ–ł–Ĺ—É, —Ä–į–≤–Ĺ—É—é 136. –Ě–į–Ļ–ī–ł—ā–Ķ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC.
–í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC –Ī–ł—Ā—Ā–Ķ–ļ—ā—Ä–ł—Ā–į BE –ł –ľ–Ķ–ī–ł–į–Ĺ–į AD –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ—č –ł –ł–ľ–Ķ—é—ā –ĺ–ī–ł–Ĺ–į–ļ–ĺ–≤—É—é –ī–Ľ–ł–Ĺ—É, —Ä–į–≤–Ĺ—É—é 136. –Ě–į–Ļ–ī–ł—ā–Ķ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC.
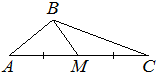 –í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ, —á—ā–ĺ AC=54, BM ‚ÄĒ –ľ–Ķ–ī–ł–į–Ĺ–į, BM=43. –Ě–į–Ļ–ī–ł—ā–Ķ AM.
–í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ, —á—ā–ĺ AC=54, BM ‚ÄĒ –ľ–Ķ–ī–ł–į–Ĺ–į, BM=43. –Ě–į–Ļ–ī–ł—ā–Ķ AM.
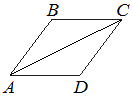 –í —Ä–ĺ–ľ–Ī–Ķ ABCD —É–≥–ĺ–Ľ ABC —Ä–į–≤–Ķ–Ĺ 146¬į. –Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–ĺ–Ľ ACD. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
–í —Ä–ĺ–ľ–Ī–Ķ ABCD —É–≥–ĺ–Ľ ABC —Ä–į–≤–Ķ–Ĺ 146¬į. –Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–ĺ–Ľ ACD. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
| α | sinα | cosα | tgα | ctgα |
| 0¬į | 0 | 1 | 0 | --- |
| 30¬į | 1/2 | √ |
√ |
√ |
| 45¬į | √ |
√ |
1 | 1 |
| 60¬į | √ |
1/2 | √ |
√ |
| 90¬į | 1 | 0 | --- | 0 |
| 120¬į | √ |
-1/2 | -√ |
0 |
| 135¬į | √ |
-√ |
-1 | -1 |
| 150¬į | 1/2 | -√ |
-√ |
-√ |
| 180¬į | 0 | -1 | 0 | --- |
| 210¬į | -1/2 | -√ |
√ |
√ |
| 225¬į | -√ |
-√ |
1 | 1 |
| 240¬į | -√ |
-1/2 | √ |
√ |
| 270¬į | -1 | 0 | --- | 0 |
| 300¬į | -√ |
1/2 | -√ |
-√ |
| 315¬į | -√ |
√ |
-1 | -1 |
| 330¬į | -1/2 | √ |
-√ |
-√ |
| 360¬į | 1 | 0 | 0 | --- |
–ö–ĺ–ľ–ľ–Ķ–Ĺ—ā–į—Ä–ł–ł: