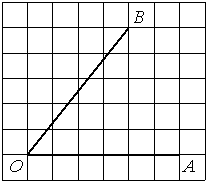
Найдите тангенс угла AOB, изображённого
на рисунке.
Проведем высоту из точки В к отрезку OA, чтобы получился
прямоугольный треугольник:
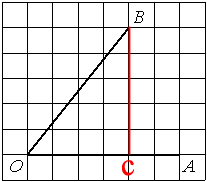Получился треугольник OBC с катетами ОС (длина 4) и BC (длина 5).
По определению тангенса:
tgAOB=BC/OC=5/4=1,25
Ответ: 1,25
Поделитесь решением
Присоединяйтесь к нам...
Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 1,8 м, высота большой опоры 2,8 м. Найдите высоту средней опоры.
В треугольнике ABC угол C равен 90°, sinA=7/17, AC=4√
Укажите номера верных утверждений.
1) Существует квадрат, который не является прямоугольником.
2) Если два угла треугольника равны, то равны и противолежащие им стороны.
3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 20, а площадь равна 50√
Найдите площадь трапеции, диагонали которой равны 15 и 7, а средняя линия равна 10.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: