Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=26.
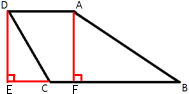Дочертим отрезки как показано на рисунке.
DE=AF, т.к. это
высоты
трапеции.
∠DCE=180°-∠BCD=180°-150°=30° (т.к. это
смежные углы).
sin(∠DCE)=ED/CD (по
определению)
sin30°=ED/CD (sin30°=1/2 по
таблице)
1/2=ED/26
ED=26*1/2=13
sin(∠ABF)=AF/AB (по
определению)
sin45°=ED/AB
AB=ED/sin45° (sin45°=√2/2 по
таблице)
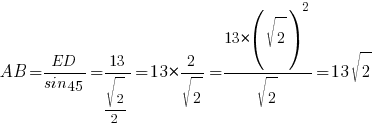
Ответ: 13√2
Поделитесь решением
Присоединяйтесь к нам...
Стороны AC, AB, BC треугольника ABC равны 3√
Докажите, что медиана треугольника делит его на два треугольника, площади которых равны между собой.
В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=14, BC=12.
Площадь равнобедренного треугольника равна 196√
Две трубы, диаметры которых равны 7 см и 24 см, требуется заменить одной, площадь поперечного сечения которой равна сумме площадей поперечных сечений двух данных. Каким должен быть диаметр новой трубы? Ответ дайте в сантиметрах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2023-03-08 21:03:16) Арина: Откуда мы узнали что синус угла ABF равен 45 градусам?