
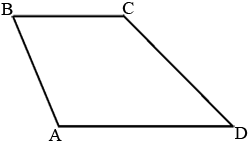
 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=32.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=32.
 Проведем
высоты, как показано на рисунке.
Проведем
высоты, как показано на рисунке.
Эти
высоты, естественно, равны друг другу.
∠DCE=∠BCD-90° (так как CE-
высота)
∠DCE=150°-90°=60°
cos∠DCE=CE/CD (по
определению косинуса).
cos60°=CE/32
CE=32cos60° (по
таблице cos60°=1/2=0,5).
CE=32*0,5=16
CE=AF=16 (как уже было сказано ранее).
sin∠ABC=AF/AB (по
определению синуса).
sin45°=16/AB
AB=16/sin45° (по
таблице sin45°=√
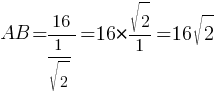
Ответ: 16√
Поделитесь решением
Присоединяйтесь к нам...
 Картинка имеет форму прямоугольника со сторонами 24 см и 37 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 1440 см2. Какова ширина окантовки? Ответ дайте в сантиметрах.
Картинка имеет форму прямоугольника со сторонами 24 см и 37 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 1440 см2. Какова ширина окантовки? Ответ дайте в сантиметрах.
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 9 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
 В треугольнике ABC угол C равен 90°, tgB=3/4, BC=12. Найдите AC.
В треугольнике ABC угол C равен 90°, tgB=3/4, BC=12. Найдите AC.
 Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен
60°. Найдите длину хорды АВ, если радиус окружности равен 8.
Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен
60°. Найдите длину хорды АВ, если радиус окружности равен 8.
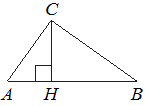 На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=2, BH=18. Найдите CH.
На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=2, BH=18. Найдите CH.





Комментарии: