Тангенс острого угла прямоугольной трапеции равен 2/9. Найдите её большее основание, если меньшее основание равно высоте и равно 54.
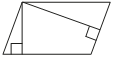
Введем обозначения ключевых точек и проведем высоту как показано на рисунке.
ABEC - квадрат, так как все углы прямые и все стороны равны.
Т.е. BE=EC=AB=54
tgα=BE/ED=2/9 (по
определению).
54/ED=2/9
ED=54*9/2=27*9=243
CD=CE+ED=54+243=297
Ответ: 297
Поделитесь решением
Присоединяйтесь к нам...
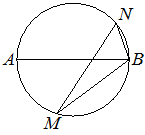На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=69°. Найдите угол NMB. Ответ дайте в градусах.
Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 16, а площадь равна 32√
Периметр квадрата равен 184. Найдите площадь квадрата.
Площадь параллелограмма равна 60, а две его стороны равны 4 и 20. Найдите его высоты. В ответе укажите большую высоту.
Найдите угол ABC. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: