
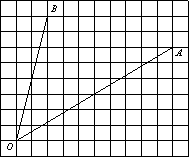
 Найдите тангенс угла AOB.
Найдите тангенс угла AOB.
Вариант №1 (Прислал пользователь Евгений)
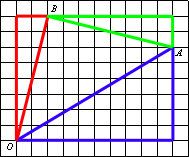 Проведем отрезок AB.
Проведем отрезок AB.
Найдем каждую сторону треугольника ABO по
теореме Пифагора:
AO2=102+62
AO2=100+36=136
AO=√
AB2=82+22
AB2=64+4=68
AB=√
BO2=82+22
BO2=64+4=68
BO=√
По
теореме косинусов:
AB2=AO2+BO2-2AO*BO*cos∠AOB
(√
68=136+68-2√
-136=-2√
68=√
68=2*2√
17=√
17=17√
1=√
cos∠AOB=1/√
По основной тригонометрической формуле:
sin2∠AOB+cos2∠AOB=1
sin2∠AOB+(1/√
sin2∠AOB+1/2=1
sin2∠AOB=1-1/2
sin2∠AOB=1/2
sin∠AOB=1/√
tg∠AOB=sin∠AOB/cos∠AOB=(1/√
Ответ: 1
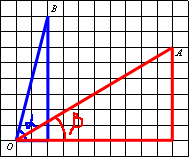 Достроим чертеж до двух
прямоугольных треугольников. Найдем
тангенсы для обоих треугольников для их углов О.
Достроим чертеж до двух
прямоугольных треугольников. Найдем
тангенсы для обоих треугольников для их углов О.Поделитесь решением
Присоединяйтесь к нам...
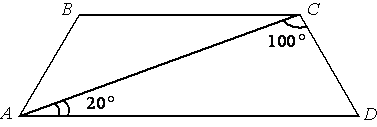 Найдите угол АВС равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.
Найдите угол АВС равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.
 Четырёхугольник ABCD описан около окружности, AB=7, BC=10, CD=14. Найдите AD.
Четырёхугольник ABCD описан около окружности, AB=7, BC=10, CD=14. Найдите AD.
 Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 8,4, а AB=4.
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 8,4, а AB=4.
 Сторона ромба равна 60, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Сторона ромба равна 60, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=66, AC=44, MN=24. Найдите AM.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=66, AC=44, MN=24. Найдите AM.





Комментарии: