В треугольнике ABC угол C равен 90°, AC=10, tgA=0,1. Найдите BC.
tdA=BC/AC (по
определению).
0,1=BC/10
BC=0,1*10=1
ответ: 1
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC известно, что ∠BAC=64°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
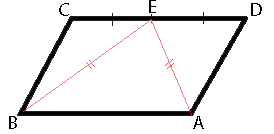В параллелограмме ABCD точка E — середина стороны CD. Известно, что EA=EB. Докажите, что данный параллелограмм — прямоугольник.
Сторона ромба равна 34, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=27, CM=9. Найдите AO.
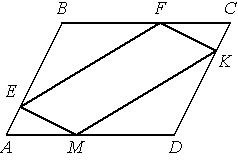В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: