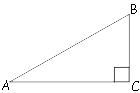
Площадь прямоугольного треугольника равна 2√
Площадь
прямоугольного треугольника равна половине произведения катетов:
S=AC*BC/2
Пусть 30-и градусам равен угол BAC.
Тангенс BAC:
td∠BAC=tg30°=BC/AC=√
BC=AC√
S=AC*(AC√
AC2/2=2
AC2=4
AC=2
Ответ: 2
Поделитесь решением
Присоединяйтесь к нам...
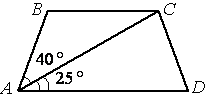Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 25° и 40° соответственно.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 10, 9 и 6. Найдите площадь параллелограмма ABCD.
Сторона ромба равна 24, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
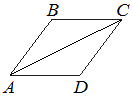В ромбе ABCD угол ABC равен 146°. Найдите угол ACD. Ответ дайте в градусах.
Какой угол (в градусах) описывает часовая стрелка за 2 часа 2 минуты?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: