
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ544 –Є–Ј 1087 |
 –Я–ї–Њ—Й–∞–і—М –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ 578√
–Я–ї–Њ—Й–∞–і—М –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ 578√
–Я–ї–Њ—Й–∞–і—М
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ –њ–Њ–ї–Њ–≤–Є–љ–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П –Ї–∞—В–µ—В–Њ–≤:
S=AC*BC/2=578√
–Я—Г—Б—В—М 30-–Є –≥—А–∞–і—Г—Б–∞–Љ —А–∞–≤–µ–љ —Г–≥–Њ–ї BAC.
–Ґ–∞–љ–≥–µ–љ—Б BAC:
td∠BAC=tg30¬∞=BC/AC=√
BC=AC√
S=AC*BC/2=578√
AC*BC=1156√
–Я–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –≤–Љ–µ—Б—В–Њ BC –Ј–љ–∞—З–µ–љ–Є–µ, –њ–Њ–ї—Г—З–µ–љ–љ–Њ–µ —А–∞–љ–µ–µ (AC√
AC*AC√
AC2=1156
AC=34
–Ю—В–≤–µ—В: 34
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C —А–∞–≤–µ–љ 90¬∞, BC=5, AC=2.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C —А–∞–≤–µ–љ 90¬∞, BC=5, AC=2.
–Э–∞–є–і–Є—В–µ tgB.
 –Ю—Б–љ–Њ–≤–∞–љ–Є—П BC –Є AD —В—А–∞–њ–µ—Ж–Є–Є ABCD —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 4 –Є 64, BD=16. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є CBD –Є ADB –њ–Њ–і–Њ–±–љ—Л.
–Ю—Б–љ–Њ–≤–∞–љ–Є—П BC –Є AD —В—А–∞–њ–µ—Ж–Є–Є ABCD —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 4 –Є 64, BD=16. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є CBD –Є ADB –њ–Њ–і–Њ–±–љ—Л.
 –Ґ–Њ—З–Ї–∞ –Ї—А–µ–њ–ї–µ–љ–Є—П —В—А–Њ—Б–∞, —Г–і–µ—А–ґ–Є–≤–∞—О—Й–µ–≥–Њ —Д–ї–∞–≥—И—В–Њ–Ї –≤ –≤–µ—А—В–Є–Ї–∞–ї—М–љ–Њ–Љ –њ–Њ–ї–Њ–ґ–µ–љ–Є–Є, –љ–∞—Е–Њ–і–Є—В—Б—П –љ–∞ –≤—Л—Б–Њ—В–µ 15 –Љ –Њ—В –Ј–µ–Љ–ї–Є. –†–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В –Њ—Б–љ–Њ–≤–∞–љ–Є—П —Д–ї–∞–≥—И—В–Њ–Ї–∞
–і–Њ –Љ–µ—Б—В–∞ –Ї—А–µ–њ–ї–µ–љ–Є—П —В—А–Њ—Б–∞ –љ–∞ –Ј–µ–Љ–ї–µ —А–∞–≤–љ–Њ 8 –Љ. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г —В—А–Њ—Б–∞. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –Љ–µ—В—А–∞—Е.
–Ґ–Њ—З–Ї–∞ –Ї—А–µ–њ–ї–µ–љ–Є—П —В—А–Њ—Б–∞, —Г–і–µ—А–ґ–Є–≤–∞—О—Й–µ–≥–Њ —Д–ї–∞–≥—И—В–Њ–Ї –≤ –≤–µ—А—В–Є–Ї–∞–ї—М–љ–Њ–Љ –њ–Њ–ї–Њ–ґ–µ–љ–Є–Є, –љ–∞—Е–Њ–і–Є—В—Б—П –љ–∞ –≤—Л—Б–Њ—В–µ 15 –Љ –Њ—В –Ј–µ–Љ–ї–Є. –†–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В –Њ—Б–љ–Њ–≤–∞–љ–Є—П —Д–ї–∞–≥—И—В–Њ–Ї–∞
–і–Њ –Љ–µ—Б—В–∞ –Ї—А–µ–њ–ї–µ–љ–Є—П —В—А–Њ—Б–∞ –љ–∞ –Ј–µ–Љ–ї–µ —А–∞–≤–љ–Њ 8 –Љ. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г —В—А–Њ—Б–∞. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –Љ–µ—В—А–∞—Е.
–Ъ–∞–Ї–Є–µ –Є–Ј –і–∞–љ–љ—Л—Е —Г—В–≤–µ—А–ґ–і–µ–љ–Є–є –≤–µ—А–љ—Л? –Ч–∞–њ–Є—И–Є—В–µ –Є—Е –љ–Њ–Љ–µ—А–∞.
1) –І–µ—А–µ–Ј –і–≤–µ —А–∞–Ј–ї–Є—З–љ—Л–µ —В–Њ—З–Ї–Є –љ–∞ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є –њ—А–Њ—Е–Њ–і–Є—В –µ–і–Є–љ—Б—В–≤–µ–љ–љ–∞—П –њ—А—П–Љ–∞—П.
2) –Т –ї—О–±–Њ–Љ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї–µ –і–Є–∞–≥–Њ–љ–∞–ї–Є –≤–Ј–∞–Є–Љ–љ–Њ –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ—Л.
3) –£ —А–∞–≤–љ–Њ—Б—В–Њ—А–Њ–љ–љ–µ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —В—А–Є –Њ—Б–Є —Б–Є–Љ–Љ–µ—В—А–Є–Є.
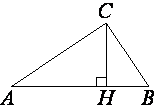 –Т –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ
ABC –Ї–∞—В–µ—В AC=8, –∞ –≤—Л—Б–Њ—В–∞ CH, –Њ–њ—Г—Й–µ–љ–љ–∞—П –љ–∞ –≥–Є–њ–Њ—В–µ–љ—Г–Ј—Г, —А–∞–≤–љ–∞ 2√
–Т –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ
ABC –Ї–∞—В–µ—В AC=8, –∞ –≤—Л—Б–Њ—В–∞ CH, –Њ–њ—Г—Й–µ–љ–љ–∞—П –љ–∞ –≥–Є–њ–Њ—В–µ–љ—Г–Ј—Г, —А–∞–≤–љ–∞ 2√





–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2018-03-11 17:32:00) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: Pavel, –њ–Њ—В–Њ–Љ—Г —З—В–Њ BC=C√
(2018-03-06 19:01:54) Pavel: AC*AC√3/3=1156√3/3 –њ–Њ—З–µ–Љ—Г –≤—Л —Г–Љ–љ–Њ–ґ–∞–µ—В–µ AC –љ–∞ AC
(2017-02-14 20:03:25) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Я–Њ–ї–Є–љ–∞, 578-x=392 => 578-392=x => x=186
(2017-02-13 14:50:35) –њ–Њ–ї–Є–љ–∞: –Ї–∞–Ї –љ–∞–є—В–Є –љ–µ –Є–Ј–≤–µ—Б—В–љ–Њ–µ —З–Є—Б–ї–Њ 578- =392
(2015-03-27 16:06:43) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Ъ–Њ—З–µ—В–Њ–≤–∞, BC —А–∞–≤–љ–Њ AC —Г–Љ–љ–Њ–ґ–µ–љ–љ–Њ–µ –љ–∞ –Ї–Њ—А–µ–љ—М –Є–Ј 3, –і–µ–ї–µ–љ–љ—Л–є –љ–∞ 3.
(2015-03-26 17:42:24) –Ї–Њ—З–µ—В–Њ–≤–∞: –њ–Њ—З–µ–Љ—Г –≤—Б=–∞—Б?