
 Катеты прямоугольного треугольника равны √
Катеты прямоугольного треугольника равны √
 Так как треугольник
прямоугольный, то можем применить
теорему Пифагора:
Так как треугольник
прямоугольный, то можем применить
теорему Пифагора:
AB2=BC2+AC2
AB2=12+(√
AB2=1+15=16
AB=4
Меньший угол лежит напротив меньшей стороны, 1<√
Ответ: 0,25
Поделитесь решением
Присоединяйтесь к нам...
 Площадь равнобедренного треугольника равна 196√
Площадь равнобедренного треугольника равна 196√
 Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76. Найдите углы ромба.
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76. Найдите углы ромба.
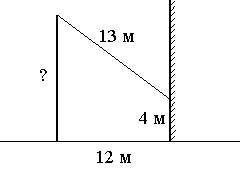 От столба к дому натянут провод длиной 13 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
От столба к дому натянут провод длиной 13 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
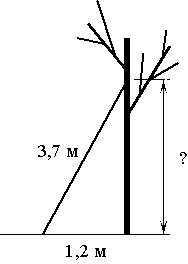 Лестницу длиной 3,7 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?
Лестницу длиной 3,7 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?
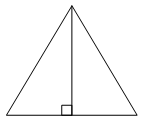 Высота равностороннего треугольника равна 78√
Высота равностороннего треугольника равна 78√





Комментарии:
(2015-03-12 18:49:47) Администратор: Дима, если AB2=16, то AB=√
(2015-03-12 15:44:47) Дима: 4 откуда ?