
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ408 –Η–Ζ 1087 |
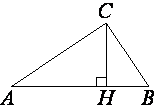 –£ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β
ABC –Κ–Α―²–Β―² AC=8, –Α –≤―΄―¹–Ψ―²–Α CH, –Ψ–Ω―É―â–Β–Ϋ–Ϋ–Α―è –Ϋ–Α –≥–Η–Ω–Ψ―²–Β–Ϋ―É–Ζ―É, ―Ä–Α–≤–Ϋ–Α 2√
–£ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β
ABC –Κ–Α―²–Β―² AC=8, –Α –≤―΄―¹–Ψ―²–Α CH, –Ψ–Ω―É―â–Β–Ϋ–Ϋ–Α―è –Ϋ–Α –≥–Η–Ω–Ψ―²–Β–Ϋ―É–Ζ―É, ―Ä–Α–≤–Ϋ–Α 2√
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Η ABC –Η ACH.
∠AHC=∠ACB (―².–Κ. ―ç―²–Ψ –Ω―Ä―è–Φ―΄–Β ―É–≥–Μ―΄).
∠A - –Ψ–±―â–Η–Ι.
–Γ–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ, –Ω–Ψ
―²–Β–Ψ―Ä–Β–Φ–Β –Ψ ―¹―É–Φ–Φ–Β ―É–≥–Μ–Ψ–≤ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ∠ACH=∠ABC
–Δ–Ψ–≥–¥–Α sin∠ACH=sin∠ABC.
–Δ–Β–Ω–Β―Ä―¨ ―Ä–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ACH.
–ü–Ψ
―²–Β–Ψ―Ä–Β–Φ–Β –ü–Η―³–Α–≥–Ψ―Ä–Α:
AC2=CH2+AH2
82=(2√
64=4*15+AH2
AH2=64-60
AH2=4
AH=2
sin∠ACH=AH/AC (–Ω–Ψ
–Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―é)
sin∠ACH=2/8=1/4=0,25
–ö–Α–Κ –±―΄–Μ–Ψ –≤―΄–≤–Β–¥–Β–Ϋ–Ψ –≤―΄―à–Β:
sin∠ABC=sin∠ACH=0,25
–û―²–≤–Β―²: sin∠ABC=0,25
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
–Γ―²–Ψ―Ä–Ψ–Ϋ―΄ AC, AB, BC ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC ―Ä–Α–≤–Ϋ―΄ 3√
 –£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC DE βÄ™ ―¹―Ä–Β–¥–Ϋ―è―è –Μ–Η–Ϋ–Η―è. –ü–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α CDE ―Ä–Α–≤–Ϋ–Α 35. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC.
–£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC DE βÄ™ ―¹―Ä–Β–¥–Ϋ―è―è –Μ–Η–Ϋ–Η―è. –ü–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α CDE ―Ä–Α–≤–Ϋ–Α 35. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC.
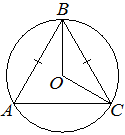 –û–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨ ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β O –Ψ–Ω–Η―¹–Α–Ϋ–Α –Ψ–Κ–Ψ–Μ–Ψ ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC, –≤ –Κ–Ψ―²–Ψ―Ä–Ψ–Φ AB=BC –Η ∠ABC=57¬Α. –ù–Α–Ι–¥–Η―²–Β –≤–Β–Μ–Η―΅–Η–Ϋ―É ―É–≥–Μ–Α BOC. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–û–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨ ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –≤ ―²–Ψ―΅–Κ–Β O –Ψ–Ω–Η―¹–Α–Ϋ–Α –Ψ–Κ–Ψ–Μ–Ψ ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC, –≤ –Κ–Ψ―²–Ψ―Ä–Ψ–Φ AB=BC –Η ∠ABC=57¬Α. –ù–Α–Ι–¥–Η―²–Β –≤–Β–Μ–Η―΅–Η–Ϋ―É ―É–≥–Μ–Α BOC. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
 –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ –Κ–≤–Α–¥―Ä–Α―²–Α, –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–≥–Ψ –≤–Ψ–Κ―Ä―É–≥ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―Ä–Α–¥–Η―É―¹–Α 83.
–ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ –Κ–≤–Α–¥―Ä–Α―²–Α, –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–≥–Ψ –≤–Ψ–Κ―Ä―É–≥ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―Ä–Α–¥–Η―É―¹–Α 83.
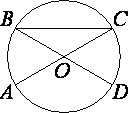 –£ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ O –Ψ―²―Ä–Β–Ζ–Κ–Η AC –Η BD βÄî –¥–Η–Α–Φ–Β―²―Ä―΄. –Π–Β–Ϋ―²―Ä–Α–Μ―¨–Ϋ―΄–Ι ―É–≥–Ψ–Μ AOD ―Ä–Α–≤–Β–Ϋ 130¬Α. –ù–Α–Ι–¥–Η―²–Β –≤–Ω–Η―¹–Α–Ϋ–Ϋ―΄–Ι ―É–≥–Ψ–Μ ACB. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–£ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η ―¹ ―Ü–Β–Ϋ―²―Ä–Ψ–Φ O –Ψ―²―Ä–Β–Ζ–Κ–Η AC –Η BD βÄî –¥–Η–Α–Φ–Β―²―Ä―΄. –Π–Β–Ϋ―²―Ä–Α–Μ―¨–Ϋ―΄–Ι ―É–≥–Ψ–Μ AOD ―Ä–Α–≤–Β–Ϋ 130¬Α. –ù–Α–Ι–¥–Η―²–Β –≤–Ω–Η―¹–Α–Ϋ–Ϋ―΄–Ι ―É–≥–Ψ–Μ ACB. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.





–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η:
(2016-05-11 09:37:59) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –û–Μ–Β―¹―è, –Κ ―¹–Ψ–Ε–Α–Μ–Β–Ϋ–Η―é, ―É –Φ–Β–Ϋ―è –Ϋ–Β―² ―²–Α–Κ–Ψ–Ι –Η–Ϋ―³–Ψ―Ä–Φ–Α―Ü–Η–Η.
(2016-05-11 09:36:57) –û–Μ–Β―¹―è: –û―²–≤–Β―²―¨―²–Β –Ω–Ψ–Ε–Α–Μ―É–Ι―¹―²–Α, –Ϋ–Α ―ç–Κ–Ζ–Α–Φ–Β–Ϋ–Β ―ç―²–Α –Ζ–Α–¥–Α―΅–Α –Ω–Ψ–¥ –Κ–Α–Κ–Η–Φ –Ϋ–Ψ–Φ–Β―Ä–Ψ–Φ. –‰–Ζ –≤―²–Ψ―Ä–Ψ–Ι ―΅–Α―¹―²–Η?
(2016-05-11 09:32:39) –û–Μ–Β―¹―è: –û―²–≤–Β―²―¨―²–Β –Ω–Ψ–Ε–Α–Μ―É–Ι―¹―²–Α, –Ϋ–Α ―ç–Κ–Ζ–Α–Φ–Β–Ϋ–Β ―ç―²–Α –Ζ–Α–¥–Α―΅–Α –Ω–Ψ–¥ –Κ–Α–Κ–Η–Φ –Ϋ–Ψ–Φ–Β―Ä–Ψ–Φ. –‰–Ζ –≤―²–Ψ―Ä–Ψ–Ι ―΅–Α―¹―²–Η?