
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ383 –Є–Ј 1087 |
–Я–ї–Њ—Й–∞–і—М –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞
722√
–Ю–±–Њ–Ј–љ–∞—З–Є–Љ:
a - –Є—Б–Ї–Њ–Љ—Л–є –Ї–∞—В–µ—В
b - –≤—В–Њ—А–Њ–є –Ї–∞—В–µ—В
c - –≥–Є–њ–Њ—В–µ–љ—Г–Ј–∞
sin30°=1/2 (
—В–∞–±–ї–Є—З–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ)
sin30¬∞=a/c=1/2 (–њ–Њ
–Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О —Б–Є–љ—Г—Б–∞)
c=2a
–Я–Њ
—В–µ–Њ—А–µ–Љ–µ –Я–Є—Д–∞–≥–Њ—А–∞:
a2+b2=c2
a2+b2=(2a)2
b2=3a2
b=a√
–Ш–Ј —Г—Б–ї–Њ–≤–Є—П: S—В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞=ab/2=722√
a*a√
–°–Њ–Ї—А–∞—Й–∞–µ–Љ √
a2=722*2=1444
a=38
–Ю—В–≤–µ—В: a=38
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ —Г–≥–ї–∞ A –і–µ–ї–Є—В –≤—Л—Б–Њ—В—Г, –њ—А–Њ–≤–µ–і–µ–љ–љ—Г—О –Є–Ј –≤–µ—А—И–Є–љ—Л B –≤ –Њ—В–љ–Њ—И–µ–љ–Є–Є 17:15, —Б—З–Є—В–∞—П –Њ—В —В–Њ—З–Ї–Є B. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC, –µ—Б–ї–Є BC=16.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ —Г–≥–ї–∞ A –і–µ–ї–Є—В –≤—Л—Б–Њ—В—Г, –њ—А–Њ–≤–µ–і–µ–љ–љ—Г—О –Є–Ј –≤–µ—А—И–Є–љ—Л B –≤ –Њ—В–љ–Њ—И–µ–љ–Є–Є 17:15, —Б—З–Є—В–∞—П –Њ—В —В–Њ—З–Ї–Є B. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC, –µ—Б–ї–Є BC=16.
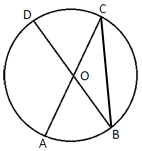 –Т –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ O AC –Є BD вАУ –і–Є–∞–Љ–µ—В—А—Л. –¶–µ–љ—В—А–∞–ї—М–љ—Л–є —Г–≥–Њ–ї AOD —А–∞–≤–µ–љ 128¬∞. –Э–∞–є–і–Є—В–µ –≤–њ–Є—Б–∞–љ–љ—Л–є —Г–≥–Њ–ї ACB. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Т –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ O AC –Є BD вАУ –і–Є–∞–Љ–µ—В—А—Л. –¶–µ–љ—В—А–∞–ї—М–љ—Л–є —Г–≥–Њ–ї AOD —А–∞–≤–µ–љ 128¬∞. –Э–∞–є–і–Є—В–µ –≤–њ–Є—Б–∞–љ–љ—Л–є —Г–≥–Њ–ї ACB. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
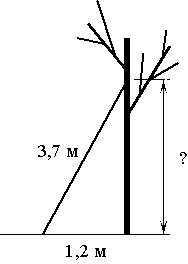 –Ы–µ—Б—В–љ–Є—Ж—Г –і–ї–Є–љ–Њ–є 3,7 –Љ –њ—А–Є—Б–ї–Њ–љ–Є–ї–Є –Ї –і–µ—А–µ–≤—Г. –Э–∞ –Ї–∞–Ї–Њ–є –≤—Л—Б–Њ—В–µ (–≤ –Љ–µ—В—А–∞—Е) –љ–∞—Е–Њ–і–Є—В—Б—П –≤–µ—А—Е–љ–Є–є –µ—С –Ї–Њ–љ–µ—Ж, –µ—Б–ї–Є –љ–Є–ґ–љ–Є–є –Ї–Њ–љ–µ—Ж –Њ—В—Б—В–Њ–Є—В –Њ—В —Б—В–≤–Њ–ї–∞ –і–µ—А–µ–≤–∞ –љ–∞ 1,2 –Љ?
–Ы–µ—Б—В–љ–Є—Ж—Г –і–ї–Є–љ–Њ–є 3,7 –Љ –њ—А–Є—Б–ї–Њ–љ–Є–ї–Є –Ї –і–µ—А–µ–≤—Г. –Э–∞ –Ї–∞–Ї–Њ–є –≤—Л—Б–Њ—В–µ (–≤ –Љ–µ—В—А–∞—Е) –љ–∞—Е–Њ–і–Є—В—Б—П –≤–µ—А—Е–љ–Є–є –µ—С –Ї–Њ–љ–µ—Ж, –µ—Б–ї–Є –љ–Є–ґ–љ–Є–є –Ї–Њ–љ–µ—Ж –Њ—В—Б—В–Њ–Є—В –Њ—В —Б—В–≤–Њ–ї–∞ –і–µ—А–µ–≤–∞ –љ–∞ 1,2 –Љ?
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –љ–∞ –µ–≥–Њ –Љ–µ–і–Є–∞–љ–µ BM –Њ—В–Љ–µ—З–µ–љ–∞ —В–Њ—З–Ї–∞ K —В–∞–Ї, —З—В–Њ BK:KM=4:1.–Я—А—П–Љ–∞—П AK –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Г BC –≤ —В–Њ—З–Ї–µ P.–Э–∞–є–і–Є—В–µ –Њ—В–љ–Њ—И–µ–љ–Є–µ –њ–ї–Њ—Й–∞–і–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABK –Ї –њ–ї–Њ—Й–∞–і–Є —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞ KPCM.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –љ–∞ –µ–≥–Њ –Љ–µ–і–Є–∞–љ–µ BM –Њ—В–Љ–µ—З–µ–љ–∞ —В–Њ—З–Ї–∞ K —В–∞–Ї, —З—В–Њ BK:KM=4:1.–Я—А—П–Љ–∞—П AK –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Г BC –≤ —В–Њ—З–Ї–µ P.–Э–∞–є–і–Є—В–µ –Њ—В–љ–Њ—И–µ–љ–Є–µ –њ–ї–Њ—Й–∞–і–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABK –Ї –њ–ї–Њ—Й–∞–і–Є —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞ KPCM.
–Я–ї–Њ—Й–∞–і—М –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞
722√





–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2015-05-04 15:53:49) –Р–ї–µ–Ї—Б–∞–љ–і—А: –Р–∞, —В–Њ—З–љ–Њ. a^2+b^2=(2a)^2 —В–Њ –µ—Б—В—М a^2+b^2=4a^2 –Є –і–∞–ї—М—И–µ b^2=-a^2+4a^2
(2015-05-04 15:50:57) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Р–ї–µ–Ї—Б–∞–љ–і—А, –Т—Л –Њ—И–Є–±–∞–µ—В–µ—Б—М:
a2+b2=(2a)2
a2+b2=4a2
b2=4a2-a2
b2=3a2
(2015-05-04 15:46:26) –Р–ї–µ–Ї—Б–∞–љ–і—А: –Я–Њ—З–µ–Љ—Г b^2+a^2=(2a)^2 –Є –њ—А–Є –њ–µ—А–µ–љ–Њ—Б–µ –≤—Л –њ–Њ–ї—Г—З–∞–µ—В–µ b^2=3a^2 –Т—Л –і–Њ–ї–ґ–љ—Л –њ–Њ–Љ–µ–љ—П—В—М –Ј–љ–∞–Ї –њ—А–Є –њ–µ—А–µ–љ–Њ—Б–µ –Є –њ–Њ–ї—Г—З–Є—В—М b^2=-a^2+2a^2