
 В треугольнике ABC угол C прямой, BC=8, sinA=0,4. Найдите AB.
В треугольнике ABC угол C прямой, BC=8, sinA=0,4. Найдите AB.
По
определению синуса sinA=BC/AB => AB=BC/sinA=8/0,4=20.
Ответ: AB=20.
Поделитесь решением
Присоединяйтесь к нам...
На какой угол (в градусах) поворачивается минутная стрелка, пока часовая проходит 21°?
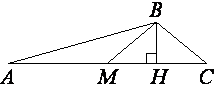 В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=216, HC=54 и ∠ACB=40°. Найдите угол AMB. Ответ дайте в градусах.
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=216, HC=54 и ∠ACB=40°. Найдите угол AMB. Ответ дайте в градусах.
Пол комнаты, имеющей форму прямоугольника со сторонами 6 м и 7 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 25 см. Сколько потребуется таких дощечек?
 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=60°. Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=60°. Найдите угол NMB. Ответ дайте в градусах.
 Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 7:6, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 48.
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 7:6, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 48.





Комментарии:
(2015-05-24 17:31:23) Администратор: Григорий, спасибо. Исправлено.
(2015-05-24 13:41:59) Григорий: в решении допущена ошибка при делении 8 на 0,4 получается 20, а не 5