Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=21, MN=14. Площадь треугольника ABC равна 27. Найдите площадь треугольника MBN.
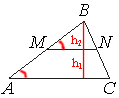Рассмотрим треугольники ABC и MBN.
∠ABC - общий.
∠BAC=∠BMN
Следовательно, по первому признаку подобия, эти треугольники подобны.
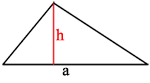
Площади треугольника ABC:
SABC=(1/2)AC*h1
27=(1/2)*21*h1
h1=27*2/21=54/21=18/7
Из подобия треугольников получаем пропорцию:
AC/MN=h1/h2
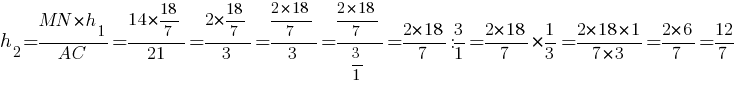
Тогда площадь треугольника MBN:
SMBN=(1/2)MN*h2
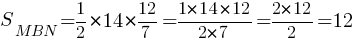
Ответ: 12
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC угол C равен 90°, AC=10, tgA=0,1. Найдите BC.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC относится к длине стороны AB как 9:7. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=44, SQ=16.
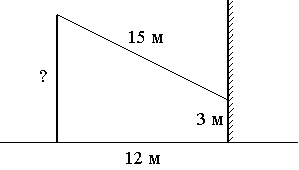От столба к дому натянут провод длиной 15 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
Периметр треугольника равен 54, одна из сторон равна 15,
а радиус вписанной в него окружности равен 1. Найдите площадь этого треугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: