Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=26.
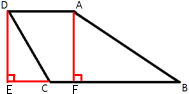Дочертим отрезки как показано на рисунке.
DE=AF, т.к. это
высоты
трапеции.
∠DCE=180°-∠BCD=180°-150°=30° (т.к. это
смежные углы).
sin(∠DCE)=ED/CD (по
определению)
sin30°=ED/CD (sin30°=1/2 по
таблице)
1/2=ED/26
ED=26*1/2=13
sin(∠ABF)=AF/AB (по
определению)
sin45°=ED/AB
AB=ED/sin45° (sin45°=√2/2 по
таблице)
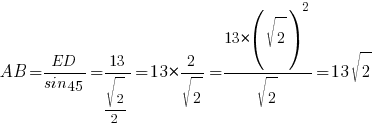
Ответ: 13√2
Поделитесь решением
Присоединяйтесь к нам...
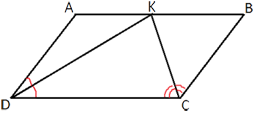Биссектрисы углов C и D параллелограмма ABCD пересекаются в точке K стороны AB. Докажите, что K — середина AB.
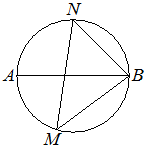На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=41°. Найдите угол NMB. Ответ дайте в градусах.
В прямоугольном треугольнике катет и гипотенуза равны 16 и 34 соответственно. Найдите другой катет этого треугольника.
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
В прямоугольном треугольнике один из катетов равен 24, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2023-03-08 21:03:16) Арина: Откуда мы узнали что синус угла ABF равен 45 градусам?