В треугольнике АВС углы А и С равны 30° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
По
теореме о сумме углов треугольника:
180°=∠A+∠B+∠C
∠B=180°-∠A-∠C=180°-30°-50°=100°.
∠ABD=∠B/2=100°/2=50° (т.к. BD -
биссектриса).
Рассмотрим треугольник BHC.
По
теореме о сумме углов треугольника:
180°=∠CHB+∠C+∠CBH=50°+90°+∠CBH
∠CBH=180°-50°-90°=40°.
Тогда искомый угол ∠DBH=∠B-∠ABD-∠CBH=100°-50°-40°=10°.
Ответ: 10
Поделитесь решением
Присоединяйтесь к нам...
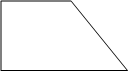Тангенс острого угла прямоугольной трапеции равен 5/3. Найдите её большее основание, если меньшее основание равно высоте и равно 40.
Проектор полностью освещает экран A высотой 100 см, расположенный на расстоянии 170 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 340 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Какие из данных утверждений верны? Запишите их номера.
1) У равнобедренного треугольника есть ось симметрии.
2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
3) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 30 см, а длина – 40 см. Найдите расстояние между точками A и B (в метрах).
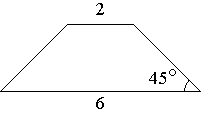В равнобедренной трапеции основания равны 2 и 6, а один из углов между боковой стороной и основанием равен
45°. Найдите площадь трапеции.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: