
 Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 3:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 41.
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 3:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 41.
Пусть AD -
биссектриса, описанная в условии.
BC - сторона, равная 41.
Рассмотрим треугольник ADC.
Для этого треугольника CO -
биссектриса,
По
свойству биссектрисы:
AO/OD=AC/CD=3/1
AC=3*CD
Рассмотрим треугольник ABD.
Для этого треугольника BO -
биссектриса,
По
свойству биссектрисы:
AO/OD=AB/BD=3/1
AB=3*BD
Складываем полученные равенства:
AC+AB=3*CD+3*BD
AC+AB=3(CD+BD), CD+BD=BC=41
AC+AB=3*41
AC+AB=123
PABC=AC+AB+BC=123+41=164
Ответ: 164
Поделитесь решением
Присоединяйтесь к нам...
 В трапеции ABCD AD=4, BC=1, а её площадь равна 35. Найдите площадь треугольника ABC.
В трапеции ABCD AD=4, BC=1, а её площадь равна 35. Найдите площадь треугольника ABC.
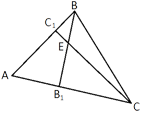 Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы BB1C1 и BCC1 равны.
Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы BB1C1 и BCC1 равны.
 Найдите площадь квадрата, описанного около окружности радиуса 32.
Найдите площадь квадрата, описанного около окружности радиуса 32.
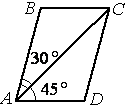 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.
 В треугольнике ABC AC=35, BC=5√
В треугольнике ABC AC=35, BC=5√



Комментарии: