В треугольнике со сторонами 16 и 2 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
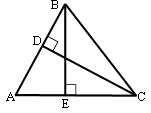Пусть AB - сторона длиной 16, а AC - сторона длиной 2.
Задачу легко решить через площадь треугольника.
Площадь треугольника равна половине произведения
высоты на сторону, к которой
высота проведена. Следовательно:
S=AB*CD/2=16*1/2=8
Так же: S=AC*BE/2
8=2*BE/2
16=2*BE
BE=8
Ответ: 8
Поделитесь решением
Присоединяйтесь к нам...
Сторона квадрата равна 6√3. Найдите площадь этого квадрата.
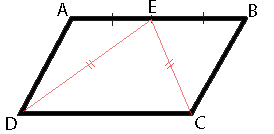В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм - прямоугольник.
Стороны AC, AB, BC треугольника ABC равны 3√
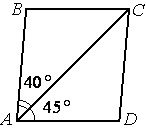Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 40°. Найдите больший угол параллелограмма.
Сторона ромба равна 20, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: