
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ480 –Є–Ј 1087 |
 –Т—Л—Б–Њ—В–∞ AH —А–Њ–Љ–±–∞ ABCD –і–µ–ї–Є—В —Б—В–Њ—А–Њ–љ—Г CD –љ–∞ –Њ—В—А–µ–Ј–Ї–Є DH=21 –Є CH=8. –Э–∞–є–і–Є—В–µ –≤—Л—Б–Њ—В—Г —А–Њ–Љ–±–∞.
–Т—Л—Б–Њ—В–∞ AH —А–Њ–Љ–±–∞ ABCD –і–µ–ї–Є—В —Б—В–Њ—А–Њ–љ—Г CD –љ–∞ –Њ—В—А–µ–Ј–Ї–Є DH=21 –Є CH=8. –Э–∞–є–і–Є—В–µ –≤—Л—Б–Њ—В—Г —А–Њ–Љ–±–∞.
AB=BC=CD=AD=DH+CH=21+8=29 (–њ–Њ
–Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О —А–Њ–Љ–±–∞).
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї AHD.
AHD -
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–є (—В.–Ї. AH -
–≤—Л—Б–Њ—В–∞), —В–Њ–≥–і–∞ –њ–Њ
—В–µ–Њ—А–µ–Љ–µ –Я–Є—Д–∞–≥–Њ—А–∞: AD2=AH2+DH2
292=AH2+212
841=AH2+441
AH2=400
AH=20
–Ю—В–≤–µ—В: AH=20
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
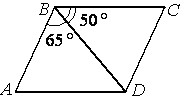 –Ф–Є–∞–≥–Њ–љ–∞–ї—М BD –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –Њ–±—А–∞–Ј—Г–µ—В —Б –µ–≥–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є —Г–≥–ї—Л, —А–∞–≤–љ—Л–µ 65¬∞ –Є 50¬∞. –Э–∞–є–і–Є—В–µ –Љ–µ–љ—М—И–Є–є —Г–≥–Њ–ї —Н—В–Њ–≥–Њ –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Ф–Є–∞–≥–Њ–љ–∞–ї—М BD –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –Њ–±—А–∞–Ј—Г–µ—В —Б –µ–≥–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є —Г–≥–ї—Л, —А–∞–≤–љ—Л–µ 65¬∞ –Є 50¬∞. –Э–∞–є–і–Є—В–µ –Љ–µ–љ—М—И–Є–є —Г–≥–Њ–ї —Н—В–Њ–≥–Њ –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
 –Ш–Ј –≤–µ—А—И–Є–љ—Л –њ—А—П–Љ–Њ–≥–Њ —Г–≥–ї–∞ C —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC –њ—А–Њ–≤–µ–і–µ–љ–∞ –≤—Л—Б–Њ—В–∞ CP. –†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ACP, —А–∞–≤–µ–љ 12 —Б–Љ, —В–∞–љ–≥–µ–љ—Б —Г–≥–ї–∞ ABC —А–∞–≤–µ–љ 2,4. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –≤–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC.
–Ш–Ј –≤–µ—А—И–Є–љ—Л –њ—А—П–Љ–Њ–≥–Њ —Г–≥–ї–∞ C —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC –њ—А–Њ–≤–µ–і–µ–љ–∞ –≤—Л—Б–Њ—В–∞ CP. –†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ACP, —А–∞–≤–µ–љ 12 —Б–Љ, —В–∞–љ–≥–µ–љ—Б —Г–≥–ї–∞ ABC —А–∞–≤–µ–љ 2,4. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –≤–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC.
 –Т —В—А–∞–њ–µ—Ж–Є–Є
ABCD AB=CD, /BDA=67¬∞ –Є /BDC=28¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї ABD. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Т —В—А–∞–њ–µ—Ж–Є–Є
ABCD AB=CD, /BDA=67¬∞ –Є /BDC=28¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї ABD. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
 –С–Њ–Ї–Њ–≤—Л–µ —Б—В–Њ—А–Њ–љ—Л AB –Є CD —В—А–∞–њ–µ—Ж–Є–Є ABCD —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 12 –Є 15, –∞ –Њ—Б–љ–Њ–≤–∞–љ–Є–µ BC —А–∞–≤–љ–Њ 3. –С–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ —Г–≥–ї–∞ ADC –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј —Б–µ—А–µ–і–Є–љ—Г —Б—В–Њ—А–Њ–љ—Л AB. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є.
–С–Њ–Ї–Њ–≤—Л–µ —Б—В–Њ—А–Њ–љ—Л AB –Є CD —В—А–∞–њ–µ—Ж–Є–Є ABCD —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 12 –Є 15, –∞ –Њ—Б–љ–Њ–≤–∞–љ–Є–µ BC —А–∞–≤–љ–Њ 3. –С–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ —Г–≥–ї–∞ ADC –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј —Б–µ—А–µ–і–Є–љ—Г —Б—В–Њ—А–Њ–љ—Л AB. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є.
 –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, –Є–Ј–Њ–±—А–∞–ґ—С–љ–љ–Њ–≥–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
–Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, –Є–Ј–Њ–±—А–∞–ґ—С–љ–љ–Њ–≥–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.



–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2017-02-20 23:56:06) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Э–∞—В–∞–ї—М—П, –і–ї—П —Н—В–Њ–≥–Њ –Є —В—А—Г–і–Є–Љ—Б—П. –°–њ–∞—Б–Є–±–Њ –Є –Т–∞–Љ.
(2017-02-20 23:15:17) –Э–∞—В–∞–ї—М—П: –Ч–∞–Љ–µ—З–∞—В–µ–ї—М–љ—Л–є —Б–∞–є—В, –≤ –≥–µ–Њ–Љ–µ—В—А–Є–Є –љ–µ —Б–Є–ї—М–љ–Њ —И–∞—А—О –∞ –≤ —Н—В–Њ–Љ –≥–Њ–і—Г –Њ–≥—Н —Б–і–∞–≤–∞—В—М –≤–∞—И —Б–∞–є—В —Б—В–∞–ї –і–ї—П –Љ–µ–љ—П –љ–∞—Е–Њ–і–Ї–Њ–є, –Њ—З–µ–љ—М –њ–Њ–і—А–Њ–±–љ–Њ –Є –њ–Њ–љ—П—В–љ–Њ –≤—Б—С –Њ–±—К—П—Б–љ—П–µ—В—Б—П ❤
(2015-02-21 12:32:03) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Т–Є–Ї—В–Њ—А–Є—П, —Б–њ–∞—Б–Є–±–Њ –Є –Т–∞–Љ –Ј–∞ —В–µ–њ–ї—Л–µ —Б–ї–Њ–≤–∞.
(2015-02-21 11:16:00) –Т–Є–Ї—В–Њ—А–Є—П: –Ъ–∞–Ї –Ј–∞–Љ–µ—З–∞—В–µ–ї—М–љ–Њ, —З—В–Њ —Б—Г—Й–µ—Б—В–≤—Г–µ—В —Н—В–Њ—В —Б–∞–є—В. –°–њ–∞—Б–Є–±–Њ –≤–∞–Љ –Њ–≥—А–Њ–Љ–љ–Њ–µ)
(2014-12-12 20:31:53) –≠–±–Њ–љ–Є—В: –љ–Њ—А–Љ
(2014-06-13 14:59:47) –і–Є–љ–∞—А–∞ : —Б–њ–∞—Б–Є–±–Њ