Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24, BF=32.
∠GAE=∠BEA (т.к. они
накрест-лежащие)
∠GAE=∠BEA=∠BAE (т.к. AE -
биссектриса).
Получается, что треугольник ABE -
равнобедренный.
BF -
биссектриса, а по
свойству равнобедренного треугольника, она так же и
медиана и
высота.
Таким образом, получается, что треугольник ABF -
прямоугольный.
По
теореме Пифагора:
AB2=AF2+BF2
AB2=242+322
AB2=576+1024=1600
AB=40
Ответ: AB=40
Поделитесь решением
Присоединяйтесь к нам...
Найдите площадь треугольника, изображённого на рисунке.
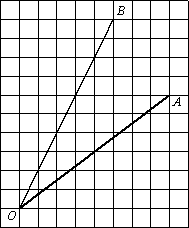Найдите тангенс угла AOB.
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
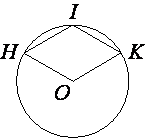Точка O – центр окружности, на которой лежат точки H, I и K таким образом, что OHIK – ромб. Найдите угол OHI. Ответ дайте в градусах.
Стороны AC, AB, BC треугольника ABC равны 3√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-03-16 21:01:20) Администратор: Евгений, тоже неплохой вариант.
(2015-03-16 19:46:19) Евгений: Проще: сумма углов А и В равна 180, а сумма половин углов равна 90, значит угол F равен 90.
(2014-11-02 11:11:00) Администратор: Эльвира, очень рад, что наш сайт помогает к подготовке, удачи на экзаменах!
(2014-11-02 09:12:26) Эльвира: Спасибо за вашу работу, за помощь в подготовке к итоговой аттестации.