Сторона AB параллелограмма ABCD вдвое больше стороны AD. Точка K — середина стороны AB. Докажите, что DK — биссектриса угла ADC.
Рассмотрим треугольник AKD.
AK=AD (по условию задачи), следовательно данный треугольник
равнобедренный.
По
свойству равнобедренного треугольника ∠ADK=∠AKD
∠AKD=∠KDC (т.к. это
накрест-лежащие углы).
Получается, что ∠ADK=∠AKD=∠KDC.
Следовательно DK -
биссектриса.
Поделитесь решением
Присоединяйтесь к нам...
На клетчатой бумаге с размером клетки 1x1 изображён параллелограмм. Найдите его площадь.
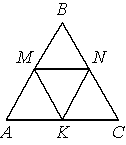В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.
В треугольнике ABC на его медиане BM отмечена точка K так, что BK:KM=10:9. Прямая AK пересекает сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника ABC.
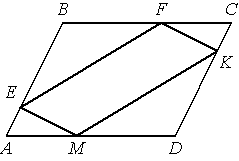В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём BF = DM, BE = DK. Докажите, что EFKM — параллелограмм.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 5 см, тангенс угла ABC равен 2,4. Найдите радиус вписанной окружности треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2014-05-26 22:01:15) Администратор: Елена, потому, что ∠ADK=∠AKD, а ∠AKD=∠KDC.
(2014-05-26 18:30:51) Елена: почему ∠ADK=∠KDC.