В трапеции ABCD AD=8, BC=5, а её площадь равна 13. Найдите площадь треугольника ABC.
Площадь
трапеции равна h*(a+b)/2, где a и b - основания трапеции, h - высота трапеции.
hтрапеции*(8+5)/2=13 (по условию задачи)
h=13/6,5=2
Проведем
высоту треугольника ABC, как показано на рисунке.
hтреугольника=hтрапеции, так как они обе перпендикулярны одним и тем же параллельным основаниям трапеции и образуют прямоугольник.
Sтреугольника=hтреугольника*BC/2=2*5/2=5
Ответ: Sтреугольника=5
Поделитесь решением
Присоединяйтесь к нам...
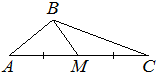В треугольнике ABC известно, что AC=38, BM — медиана, BM=17. Найдите AM.
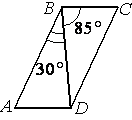Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 85° и 30°. Найдите меньший угол параллелограмма.
Стороны AC, AB, BC треугольника ABC равны 3√
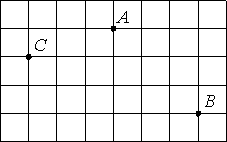На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
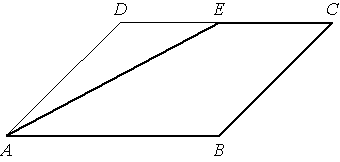Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-12-24 19:18:01) флюра: спасибо. очень удобно.