
Какие из данных утверждений верны? Запишите их номера.
1) Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) У равностороннего треугольника есть центр симметрии.
Рассмотрим каждое утверждение.
1) "Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны"? это утверждение верно по
первому признаку подобия.
2) "В любом прямоугольнике диагонали взаимно перпендикулярны", это утверждение неверно. Из прямоугольников, только у квадрата диагонали перпендикулярны (
свойство квадрата, которого нет у прямоугольников).
3) "У равностороннего треугольника есть
центр симметрии", это утверждение неверно. Есть три
оси симметрии, совпадающих с любой из
высот
равностороннего треугольника.
Поделитесь решением
Присоединяйтесь к нам...
 Площадь прямоугольного треугольника равна 128√
Площадь прямоугольного треугольника равна 128√
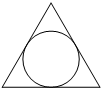 Сторона равностороннего треугольника равна 2√
Сторона равностороннего треугольника равна 2√
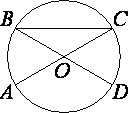 В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 132°. Найдите вписанный угол ACB. Ответ дайте в градусах.
В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 132°. Найдите вписанный угол ACB. Ответ дайте в градусах.
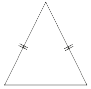 Боковая сторона равнобедренного треугольника равна 25, а основание равно 30. Найдите площадь этого треугольника.
Боковая сторона равнобедренного треугольника равна 25, а основание равно 30. Найдите площадь этого треугольника.
 Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.



Комментарии: