На окружности отмечены точки A и B так, что меньшая дуга AB равна 66°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
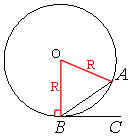Проведем радиусы к точкам A и B, как показано на рисунке.
∠AOB - центральный и опирается на дугу в 66°, следовательно:
∠AOB=66°
Треугольник AOB - равнобедренный, так как две его стороны - это радиусы окружности.
Тогда, по свойству равнобедренного треугольника, углы при основании равны, обозначим их α.
По
теореме о сумме углов треугольника:
∠AOB+∠OAB+∠OBA=180°
66°+α+α=180°
2α=180°-66°=114°
α=114°/2=57°
По
свойству касательной ∠OBC=90°.
∠ABC=∠OBC-∠OBA
∠ABC=90°-57°=33°
Ответ: 33
Поделитесь решением
Присоединяйтесь к нам...
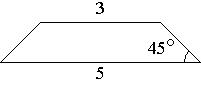В равнобедренной трапеции основания равны 3 и 5, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=9. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
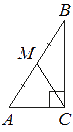В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=60, BC=40. Найдите CM.
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 57.
Радиус вписанной в квадрат окружности равен 2√2. Найдите радиус окружности, описанной около этого квадрата.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: