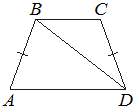
В трапеции ABCD известно, что AB=CD, ∠BDA=38° и ∠BDC=32°. Найдите угол ABD. Ответ дайте в градусах.
Трапеция ABCD
равнобедренная, так как AB=CD.
Следовательно, по второму свойству равнобедренной трапеции:
∠BAD=∠CDA=∠BDA+∠BDC=38°+32°=70°
Рассмотрим треугольник ABD.
По
теореме о сумме углов треугольника:
180°=∠BAD+∠BDA+∠ABD
180°=70°+38°+∠ABD
∠ABD=180°-70°-38°=72°
Ответ: 72
Поделитесь решением
Присоединяйтесь к нам...
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника AMK.
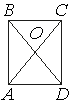Диагонали AC и BD прямоугольника ABCD пересекаются
в точке O, BO=37, AB=56. Найдите AC.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 60, тангенс угла BAC равен 5/12. Найдите радиус окружности, вписанной в треугольник ABC.
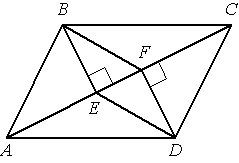В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что треугольники BEF и DFE равны.
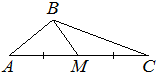В треугольнике ABC известно, что AC=38, BM — медиана, BM=17. Найдите AM.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: