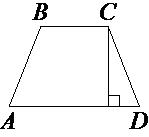Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 1 и 5. Найдите длину основания BC.
Проведем отрезок из точки B перпендикулярно AD, как показано на рисунке.
BCEF - прямоугольник.
Рассмотрим треугольники ABF и DCE.
∠BAF=∠CDE (по второму свойству равнобедренной трапеции).
∠BFA=∠CED=90°
Следовательно, ∠ABF=∠DCE (по теореме о сумме углов треугольника).
AB=CD (по определению равнобедренной трапеции).
Тогда, по второму признаку данные треугольники равны.
Следовательно AF=DE=1.
FE=AE-DE=5-1=4
BC=FE=4 (по свойству прямоугольника).
Ответ: 4
Поделитесь решением
Присоединяйтесь к нам...
В трапецию, сумма длин боковых сторон которой равна 18, вписана окружность. Найдите длину средней линии трапеции.
Имеются два сосуда, содержащие 12 кг и 8 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 65% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60% кислоты. Сколько килограммов кислоты содержится во втором растворе?
Радиус окружности с центром в точке O равен 50, длина хорды AB равна 96 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
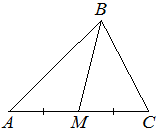В треугольнике ABC известно, что AC=14, BM — медиана, BM=10. Найдите AM.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: