Укажите номера верных утверждений.
1) В тупоугольном треугольнике все углы тупые.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
Рассмотрим каждое утверждение.
1) В тупоугольном треугольнике все углы тупые.
Тупой угол - это угол больше 90°. Если утверждение верно, то сумма углов тупоугольного треугольника будет дольше 270°. А это не верно, т.к. противоречит теореме о сумме углов треугольника. Утверждение неверно.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам. Это утверждение верно, т.к. это свойство параллелограмма.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка. Это утверждение верно, т.к. это свойство серединного перпендикуляра (другое название - медиатрисса).
Ответ: 2), 3)
Поделитесь решением
Присоединяйтесь к нам...
В трапеции ABCD основания AD и BC равны соответственно 33 и 11,
а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.
Какие из данных утверждений верны? Запишите их номера.
1) Любой параллелограмм можно вписать в окружность.
2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.
3) Точка пересечения двух окружностей равноудалена от центров этих окружностей.
В треугольнике ABC угол C равен 90°, sinA=8/9, AC=2√
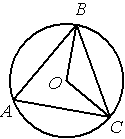Точка О – центр окружности, /BAC=20° (см. рисунок). Найдите величину угла BOC (в градусах).
Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является его медианой.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: