Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен
60°. Найдите длину хорды АВ, если радиус окружности равен 8.
Рассмотрим треугольник АОВ.
АО=ОВ, т.к. это радиусы окружности.
Следовательно, треугольник АОВ - равнобедренный.
Это значит, что ∠ОВА = ∠ОАВ = 60° (по свойству равнобедренного треугольника). Заметим, что ∠АОВ тоже равен 60° (по теореме о сумме углов треугольника). 180°-60°-60°=60°.
Следовательно, треугольник АОВ - равносторонний (по свойству равностороннего треугольника).
Получается, что ОВ=ОА=АВ=8.
Ответ: 8
Поделитесь решением
Присоединяйтесь к нам...
Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной CD углы, равные
30° и 105° соответственно.
Какие из следующих утверждений верны?
1) Один из двух смежных углов острый, а другой тупой.
2) Площадь квадрата равна произведению двух его смежных сторон.
3) Все хорды одной окружности равны между собой.
Биссектрисы углов B и C трапеции ABCD пересекаются в точке O, лежащей на стороне AD. Докажите, что точка O равноудалена от прямых AB, BC и CD.
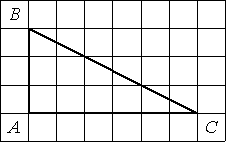Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: