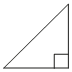
В прямоугольном треугольнике один из катетов равен 7, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
По
теореме о сумме углов треугольника можно вычислить третий угол, он равен 180°-90°-45°=45°.
Следовательно, этот треугольник
равнобедренный (по первому
свойству).
Т.е. катеты этого треугольника равны.
Площадь
прямоугольного треугольника = ab/2, где а и b - катеты. Тогда:
Sтреугольника=7*7/2=24,5
Ответ: Sтреугольника=24,5
Поделитесь решением
Присоединяйтесь к нам...
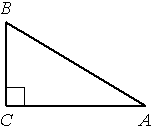В треугольнике ABC угол C прямой, BC=9, sinA=0,3. Найдите AB.
На стороне BC прямоугольника ABCD, у которого AB=12 и AD=17, отмечена точка E так, что
/EAB=45°. Найдите ED.
Площадь прямоугольного треугольника равна 8√
Основания трапеции равны 5 и 40, одна из боковых сторон равна 14, а косинус угла между ней и одним из оснований равен 3/5. Найдите площадь трапеции.
Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 16,5 см, а длина – 28 см. Найдите расстояние между точками A и B (в метрах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: