
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ605 –Є–Ј 1087 |
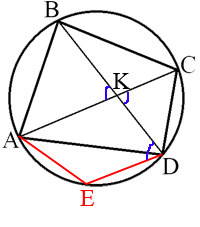 –І–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї ABCD —Б–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є AB=19 –Є CD=22 –≤–њ–Є—Б–∞–љ –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Ф–Є–∞–≥–Њ–љ–∞–ї–Є AC –Є BD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K, –њ—А–Є—З—С–Љ вИ†AKB=60¬∞. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ —Н—В–Њ–≥–Њ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
–І–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї ABCD —Б–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є AB=19 –Є CD=22 –≤–њ–Є—Б–∞–љ –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Ф–Є–∞–≥–Њ–љ–∞–ї–Є AC –Є BD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K, –њ—А–Є—З—С–Љ вИ†AKB=60¬∞. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ —Н—В–Њ–≥–Њ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
–Я—Г—Б—В—М R - —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є.
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї BCA.
–≠—В–Њ—В —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї –≤–њ–Є—Б–∞–љ –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, —В–Њ–≥–і–∞ –њ–Њ
—В–µ–Њ—А–µ–Љ–µ —Б–Є–љ—Г—Б–Њ–≤:
AB/sin(∠BCA)=2R
AB=2Rsin(∠BCA)
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї BCD.
–≠—В–Њ—В —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї —В–Њ–ґ–µ –≤–њ–Є—Б–∞–љ –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, —В–Њ–≥–і–∞ –њ–Њ
—В–µ–Њ—А–µ–Љ–µ —Б–Є–љ—Г—Б–Њ–≤:
CD/sin(∠CBD)=2R
CD=2Rsin(∠CBD)
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї BCK.
–Я–Њ
—В–µ–Њ—А–µ–Љ–µ –Њ —Б—Г–Љ–Љ–µ —Г–≥–ї–Њ–≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞:
∠CBD+∠BCA+∠CKB=180¬∞
∠AKB - —П–≤–ї—П–µ—В—Б—П —Б–Љ–µ–ґ–љ—Л–Љ –њ–Њ –Њ—В–љ–Њ—И–µ–љ–Є—О –Ї ∠CKB, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ ∠CKB=180¬∞-∠AKB. –Я–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –≤ —Г—А–∞–≤–љ–µ–љ–Є–µ –≤—Л—И–µ:
∠CBD+∠BCA+(180¬∞-∠AKB)=180¬∞
∠CBD+∠BCA+(180¬∞-60¬∞)=180¬∞
∠CBD+∠BCA=60¬∞
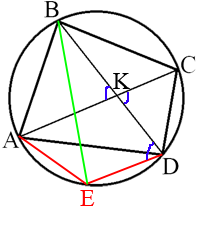 –Ф–ї—П –њ—А–Њ—Б—В–Њ—В—Л –Њ–±–Њ–Ј–љ–∞—З–Є–Љ ∠CBD=–∞ –Є ∠BCA=b, —В.–µ. a+b=60¬∞
–Ф–ї—П –њ—А–Њ—Б—В–Њ—В—Л –Њ–±–Њ–Ј–љ–∞—З–Є–Љ ∠CBD=–∞ –Є ∠BCA=b, —В.–µ. a+b=60¬∞
a=60°-b
19=AB=2Rsin(a)
22=CD=2Rsin(60¬∞-a)=2R(sin60¬∞cos(a)-cos60¬∞sin(a))=2R((√
–†–∞–Ј–і–µ–ї–Є–Љ –≤—В–Њ—А–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –љ–∞ –њ–µ—А–≤–Њ–µ:
19/22=R(√
19/22=(√
19*2sin(a)=22*(√
38sin(a)=22√
60sin(a)=22√
–Т–Њ–Ј–≤–µ–і–µ–Љ –њ—А–∞–≤—Г—О –Є –ї–µ–≤—Г—О —З–∞—Б—В–Є –≤ –Ї–≤–∞–і—А–∞—В:
3600sin2(a)=484*3cos2(a)
3600sin2(a)=1452(1-sin2(a)) (–њ—А–Є–Љ–µ–љ–µ–љ–∞
–Њ—Б–љ–Њ–≤–љ–∞—П —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–∞—П —Д–Њ—А–Љ—Г–ї–∞)
3600sin2(a)=1452-1452sin2(a))
5052sin2(a)=1452
sin2(a)=1452/5052
sin2(a)=484/1684
sin2(a)=121/421
sin(a)=√
sin(a)=11/√
22=2R*11/(√
1=R/(√
R=√
–Ю—В–≤–µ—В: R=√
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 –С–Њ–Ї–Њ–≤—Л–µ —Б—В–Њ—А–Њ–љ—Л AB –Є CD —В—А–∞–њ–µ—Ж–Є–Є ABCD —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 12 –Є 15, –∞ –Њ—Б–љ–Њ–≤–∞–љ–Є–µ BC —А–∞–≤–љ–Њ 3. –С–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ —Г–≥–ї–∞ ADC –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј —Б–µ—А–µ–і–Є–љ—Г —Б—В–Њ—А–Њ–љ—Л AB. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є.
–С–Њ–Ї–Њ–≤—Л–µ —Б—В–Њ—А–Њ–љ—Л AB –Є CD —В—А–∞–њ–µ—Ж–Є–Є ABCD —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 12 –Є 15, –∞ –Њ—Б–љ–Њ–≤–∞–љ–Є–µ BC —А–∞–≤–љ–Њ 3. –С–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ —Г–≥–ї–∞ ADC –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј —Б–µ—А–µ–і–Є–љ—Г —Б—В–Њ—А–Њ–љ—Л AB. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є.
 –Т—Л—Б–Њ—В–∞ BH —А–Њ–Љ–±–∞ ABCD –і–µ–ї–Є—В –µ–≥–Њ —Б—В–Њ—А–Њ–љ—Г AD –љ–∞ –Њ—В—А–µ–Ј–Ї–Є AH=21 –Є HD=8. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —А–Њ–Љ–±–∞.
–Т—Л—Б–Њ—В–∞ BH —А–Њ–Љ–±–∞ ABCD –і–µ–ї–Є—В –µ–≥–Њ —Б—В–Њ—А–Њ–љ—Г AD –љ–∞ –Њ—В—А–µ–Ј–Ї–Є AH=21 –Є HD=8. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —А–Њ–Љ–±–∞.
 –£–≥–ї—Л –њ—А–Є –Њ–і–љ–Њ–Љ –Є–Ј –Њ—Б–љ–Њ–≤–∞–љ–Є–є —В—А–∞–њ–µ—Ж–Є–Є —А–∞–≤–љ—Л 48¬∞ –Є 42¬∞, –∞ –Њ—В—А–µ–Ј–Ї–Є, —Б–Њ–µ–і–Є–љ—П—О—Й–Є–µ —Б–µ—А–µ–і–Є–љ—Л –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ—Л—Е —Б—В–Њ—А–Њ–љ —В—А–∞–њ–µ—Ж–Є–Є —А–∞–≤–љ—Л 6 –Є 3. –Э–∞–є–і–Є—В–µ –Њ—Б–љ–Њ–≤–∞–љ–Є—П —В—А–∞–њ–µ—Ж–Є–Є.
–£–≥–ї—Л –њ—А–Є –Њ–і–љ–Њ–Љ –Є–Ј –Њ—Б–љ–Њ–≤–∞–љ–Є–є —В—А–∞–њ–µ—Ж–Є–Є —А–∞–≤–љ—Л 48¬∞ –Є 42¬∞, –∞ –Њ—В—А–µ–Ј–Ї–Є, —Б–Њ–µ–і–Є–љ—П—О—Й–Є–µ —Б–µ—А–µ–і–Є–љ—Л –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ—Л—Е —Б—В–Њ—А–Њ–љ —В—А–∞–њ–µ—Ж–Є–Є —А–∞–≤–љ—Л 6 –Є 3. –Э–∞–є–і–Є—В–µ –Њ—Б–љ–Њ–≤–∞–љ–Є—П —В—А–∞–њ–µ—Ж–Є–Є.
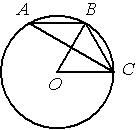 –Ґ–Њ—З–Ї–∞ –Ю вАУ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, /BOC=60¬∞ (—Б–Љ. —А–Є—Б—Г–љ–Њ–Ї). –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ BAC (–≤ –≥—А–∞–і—Г—Б–∞—Е).
–Ґ–Њ—З–Ї–∞ –Ю вАУ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, /BOC=60¬∞ (—Б–Љ. —А–Є—Б—Г–љ–Њ–Ї). –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ BAC (–≤ –≥—А–∞–і—Г—Б–∞—Е).
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C –њ—А—П–Љ–Њ–є, BC=6, sinA=0,6. –Э–∞–є–і–Є—В–µ AB.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C –њ—А—П–Љ–Њ–є, BC=6, sinA=0,6. –Э–∞–є–і–Є—В–µ AB.
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є: