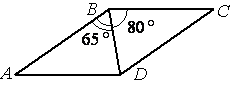Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 80°. Найдите меньший угол параллелограмма.
По
свойству
параллелограмма /B=/D=65°+80°=145° и /A=/C.
Найдем углы A и C.
Стороны AD и BC параллельны (по
определению параллелограмма). Если рассмотреть BD как секущую к этим параллельным прямым, то становится очевидным, что /CBD=/ADB=80° (т.к. они
накрест лежащие).
Рассмотрим треугольник ABD.
По
теореме о сумме углов треугольника мы можем написать: 180°=/ABD+/BDA+/A
180°=65°+80°+/A
/A=35°=/C
145>35, следовательно углы A и C - меньшие.
Ответ: меньший угол равен 35°.
Поделитесь решением
Присоединяйтесь к нам...
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=21, BF=20.
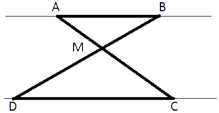Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=16, DC=24, AC=25.
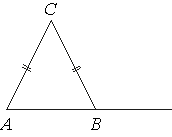В треугольнике ABC AC=BC. Внешний угол при вершине B равен 121°. Найдите угол C. Ответ дайте в градусах.
Прямая касается окружности в точке K. Центр окружности – точка O. Хорда KM образует с касательной угол, равный 40°. Найдите величину угла KOM. Ответ дайте в градусах.
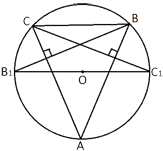Высоты остроугольного треугольника ABC, проведённые из точек B и C, продолжили до пересечения с описанной окружностью в точках B1 и C1. Оказалось, что отрезок B1C1 проходит через центр описанной окружности. Найдите угол BAC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: