Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.
Рассмотрим рисунок. Проведем отрезок MP, как показано на рисунке. BM - диаметр малой окружности (по условию задачи), следовательно треугольник BMP -
прямоугольный с гипотенузой BM (по
свойству описанной окружности).
Рассмотрим треугольники BMP и CPM:
MP - общая сторона
BP=PC (по условию задачи)
/BPM=/CPM, т.к. /BPM - прямой, а /CPM - ему
смежный.
Следовательно треугольники BMP и CPM равны (по
первому признаку). Отсюда следует, что BM=MC=MA.
Рассмотрим треугольник BMC. Т.к. MB=MC, то этот треугольник
равнобедренный, следовательно /MCP=/PBM (по
свойству равнобедренных треугольников).
В треугольнике ABM аналогичная ситуация, /BAM=/ABM.
Т.е. получается, что /BAM+/MCP=/ABC. Из
теоремы о сумме углов треугольника следует, 180°=/BAM+/MCP+/ABC
180°=/ABC+/ABC
180°=2*/ABC
90°=/ABC
Из чего следует, что треугольник ABC -
прямоугольный. По
свойству описанной окружности следует, что точка М - центр окружности, следовательно AC - диаметр => AC=2*R=2*7=14.
Ответ: AC=14.
Поделитесь решением
Присоединяйтесь к нам...
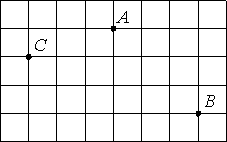На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
Высота BH ромба ABCD делит его сторону AD на отрезки AH=21 и HD=54. Найдите площадь ромба.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
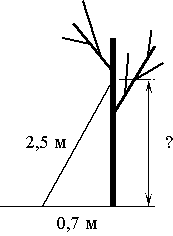Лестницу длиной 2,5 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 0,7 м?
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=3 и MB=12. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: