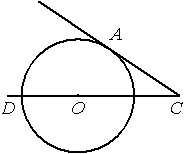
Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
130°.
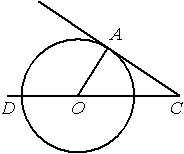Проведем отрезок ОА.
/DOA -
центральный угол для данной окружности. Он опирается на дугу AD, равную 130°. Следовательно, /DOA тоже равен 130°.
/AOC -
смежный углу DOA, поэтому /AOC=180°- /DOA=180°-130°=50°.
Треугольник ACO -
прямоугольный, т.к. радиус всегда перпендикулярен
касательной (по
свойству касательной). Т.е. /ОАС=90°. Применяя
теорему о сумме углов треугольника, можем записать:
180°=/AСO+/CAO+/AOC.
/AСO=180°-/CAO-/AOC=180°-90°-50°=40°.
Ответ: /ACO=40°.
Поделитесь решением
Присоединяйтесь к нам...
Площадь параллелограмма равна 60, а две его стороны равны 4 и 20. Найдите его высоты. В ответе укажите большую высоту.
Точка O – центр окружности, на которой лежат точки S, T и V таким образом, что OSTV – ромб. Найдите угол OVT. Ответ дайте в градусах.
Какие из следующих утверждений верны?
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Диагонали ромба равны.
3) Тангенс любого острого угла меньше единицы.
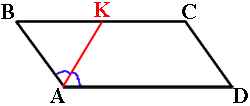Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=6, CK=10.
Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 3. Найдите радиус окружности.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: