Сторона ромба равна 24, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
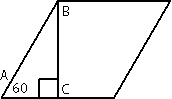Рассмотрим треугольник АВС, этот треугольник
прямоугольный (по условию задачи). /A=60°, следовательно по
теореме о сумме углов треугольника /АВС = 180°-90°-60°=30°. По
свойству прямоугольного треугольника АС=АВ/2=24/2=12. Следовательно вторая половина стороны ромба = 24-12=12. Т.е., в данной задаче, высота, проведенная к стороне ромба делит эту сторону на две равные части.
Ответ: длины обоих отрезков равны 12.
Поделитесь решением
Присоединяйтесь к нам...
Радиус окружности с центром в точке O равен 50, длина хорды AB равна 96 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.
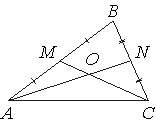Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=21, CM=15. Найдите OM.
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 17, а одна из диагоналей ромба равна 68. Найдите углы ромба.
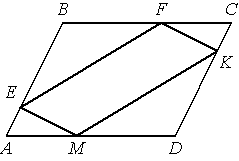В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём BF = DM, BE = DK. Докажите, что EFKM — параллелограмм.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: