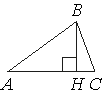В остроугольном треугольнике ABC проведена высота BH, ∠BAC=37°. Найдите угол ABH. Ответ дайте в градусах.
Рассмотрим треугольник ABH.
Это
прямоугольный треугольник, так как BH -
высота.
Тогда, по теореме о сумме углов треугольника:
180°=∠ABH+∠AHB+∠BAH
∠BAH=∠BAC=37° (так как это один и тот же угол).
180°=∠ABH+90°+37°
180°-90°-37°=∠ABH
∠ABH=53°
Ответ: 53
Поделитесь решением
Присоединяйтесь к нам...
Человек, рост которого равен 1,6 м, стоит на расстоянии 3 м от уличного фонаря. При этом длина тени человека равна 2 м. Определите высоту фонаря (в метрах).
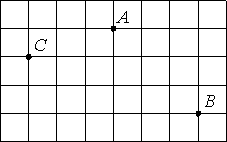На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АС, если сторона АВ равна 3.
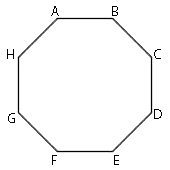ABCDEFGH – правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
Прямые m и n параллельны. Найдите ∠3, если ∠1=6°, ∠2=101°. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: