В треугольнике ABC угол C равен 90°, sinB=4/9, AB=18. Найдите AC.
По
определению синуса:
sinB=AC/AB
AC=AB*sinB=18*4/9=(18*4)/9=2*4=8
Ответ: 8
Поделитесь решением
Присоединяйтесь к нам...
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=17 и MB=19. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 164. Найдите стороны треугольника ABC.
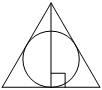Радиус окружности, вписанной в равносторонний треугольник, равен 5. Найдите высоту этого треугольника.
Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD=10. Докажите, что треугольники CBD и BDA подобны.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2024-05-07 23:09:48) Даниил: 113