Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит меньший угол.
2) Любой квадрат можно вписать в окружность.
3) Площадь трапеции равна произведению средней линии на высоту.
Рассмотрим каждое утверждение.
1) "Против большей стороны треугольника лежит меньший угол", это утверждение неверно, т.к. противоречит
теореме о соотношении углов и сторон.
2) "Любой
квадрат можно вписать в
окружность", это утверждение верно, т.к. четырехугольник можно вписать в окружность, если сумма противоположных углов этого четырехугольника равна 180°.
3) "Площадь
трапеции равна произведению
средней линии на высоту", это утверждение верно.
Поделитесь решением
Присоединяйтесь к нам...
Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.
Найдите площадь параллелограмма, изображённого на рисунке.
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 45 и 46, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 120°, а CD=34.
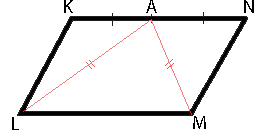В параллелограмме KLMN точка A — середина стороны KN. Известно, что AL=AM. Докажите, что данный параллелограмм — прямоугольник.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: