
 Радиус окружности, вписанной в трапецию, равен 32. Найдите высоту этой трапеции.
Радиус окружности, вписанной в трапецию, равен 32. Найдите высоту этой трапеции.
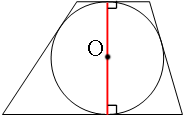 Проведем радиусы к точкам касания с основаниями трапеции.
Проведем радиусы к точкам касания с основаниями трапеции.
По первому свойству касательной (основания трапеции), она перпендикулярна радиусу.
Так как радиусы одновременно перпендикулярны параллельным основаниям трапеции, то получается, что радиусы представляют из себя единый отрезок или диаметр (это можно доказать если рассмотреть углы при параллельных прямых и секущей. Прямые углы являются односторонними и их сумма равна 180°).
Диаметр и является высотой трапеции:
h=D=2*R=2*32=64
Ответ: 64
Поделитесь решением
Присоединяйтесь к нам...
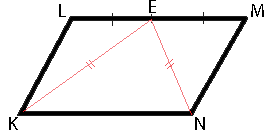 В параллелограмме KLMN точка E — середина стороны LM. Известно, что EK=EN. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме KLMN точка E — середина стороны LM. Известно, что EK=EN. Докажите, что данный параллелограмм — прямоугольник.
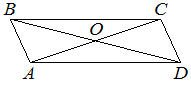 Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=24, BD=28, AB=6. Найдите DO.
Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=24, BD=28, AB=6. Найдите DO.
 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
 Боковые стороны AB и CD трапеции ABCD равны соответственно 20 и 25, а основание BC равно 5. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Боковые стороны AB и CD трапеции ABCD равны соответственно 20 и 25, а основание BC равно 5. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
 Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 10. Найдите BC, если AC=16.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 10. Найдите BC, если AC=16.
Комментарии: