
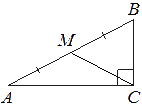
 В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=20, BC=10. Найдите CM.
В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=20, BC=10. Найдите CM.
Первый вариант решения
 Так как треугольник ABC прямоугольный, то воспользуемся теоремой об описанной окружности для прямоугольного треугольника. Для этого опишем окружность вокруг треугольника ABC.
Так как треугольник ABC прямоугольный, то воспользуемся теоремой об описанной окружности для прямоугольного треугольника. Для этого опишем окружность вокруг треугольника ABC.
Центр описанной вокруг прямоугольного треугольника окружности лежит на середине гипотенузы.
Получается, что точка М и есть центр окружности, следовательно:
R=AM=MB=AB/2=20/2=10
CM тоже является радиусом окружности, т.е.:
CM=R=10
Ответ: 10
Поделитесь решением
Присоединяйтесь к нам...
 Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
 В треугольнике ABC проведена биссектриса AL, угол ALC равен 52°, угол ABC равен 13°. Найдите угол ACB. Ответ дайте в градусах.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 52°, угол ABC равен 13°. Найдите угол ACB. Ответ дайте в градусах.
 Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды
CD, если AB=12, CD=16, а расстояние от центра окружности до хорды AB равно 8.
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды
CD, если AB=12, CD=16, а расстояние от центра окружности до хорды AB равно 8.
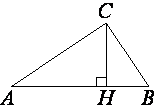 В прямоугольном треугольнике ABC катет AC=65, а высота CH, опущенная на гипотенузу, равна 13√
В прямоугольном треугольнике ABC катет AC=65, а высота CH, опущенная на гипотенузу, равна 13√
 Площадь прямоугольного треугольника равна 50√
Площадь прямоугольного треугольника равна 50√
Комментарии:
(2021-10-17 20:32:36) Администратор: Елена, здравствуйте. Видимо, условие - это шаблон для составления целой серии задач с разными вопросами. В данном случае длина катета не пригодилась, в другом, возможно, понадобится...
(2021-10-17 06:52:52) Елена: Здравствуйте. Зачем дана длина катета?
(2021-10-14 18:20:28) Администратор: Денис, согласен с вами, добавил ваш вариант.
(2021-03-25 20:57:33) Денис.: Зачем всё так усложнять?Не легче просто воспользоваться правилом ,то что в прямоугольном треугольнике медиана проведенная к гипотенузе равна половине гипотенузы
(2020-04-15 11:20:54) Администратор: Александра, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2020-04-12 19:50:28) Александра: в треугольнике авс угол с равен 90 М- середина стороны ав, ав=64 вс=44 найти см
(2019-03-22 18:27:58) Администратор: Миша, решение перед вами, уточните, пожалуйста, вопрос.
(2019-03-20 23:29:13) миша: а почему в ответе 10