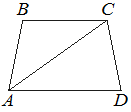
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 46° и 1° соответственно. Ответ дайте в градусах.
По
свойству равнобедренной трапеции, углы при основании равны.
Т.е. ∠B=∠C - это и есть наибольшие углы.
∠A=∠BAC+∠DAC=1°+46°=47°
AD||BC (по определению трапеции), следовательно боковую сторону AB можно рассматривать как секущую.
Тогда:
∠A+∠B=180° (так как это
внутренние углы).
∠B=180°-∠A=180°-47°=133°
Ответ: 133
Поделитесь решением
Присоединяйтесь к нам...
На отрезке AB выбрана точка C так, что AC=12 и BC=3. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
Какой угол (в градусах) описывает часовая стрелка за 2 часа 2 минуты?
Укажите номера верных утверждений.
1) Существует прямоугольник, который не является параллелограммом.
2) Треугольник с углами 40° , 70°, 70° — равнобедренный.
3) Если из точки M проведены две касательные к окружности и А и В — точки касания, то отрезки MA и MB равны.
В треугольнике ABC угол C равен 45°, AB=6√
Площадь прямоугольного треугольника равна 8√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: