
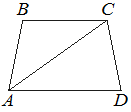
 Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 46° и 1° соответственно. Ответ дайте в градусах.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 46° и 1° соответственно. Ответ дайте в градусах.
По
свойству равнобедренной трапеции, углы при основании равны.
Т.е. ∠B=∠C - это и есть наибольшие углы.
∠A=∠BAC+∠DAC=1°+46°=47°
AD||BC (по определению трапеции), следовательно боковую сторону AB можно рассматривать как секущую.
Тогда:
∠A+∠B=180° (так как это
внутренние углы).
∠B=180°-∠A=180°-47°=133°
Ответ: 133
Поделитесь решением
Присоединяйтесь к нам...
 Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=24, BC=18. Найдите AD.
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=24, BC=18. Найдите AD.
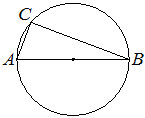 Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если
угол BAC равен 74°. Ответ дайте в градусах.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если
угол BAC равен 74°. Ответ дайте в градусах.
 Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 72°. Найдите величину угла OMK. Ответ дайте в градусах.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 72°. Найдите величину угла OMK. Ответ дайте в градусах.
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=64°. Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=64°. Найдите угол NMB. Ответ дайте в градусах.
Комментарии: