
 Периметр треугольника равен 50, одна из сторон равна 20,
а радиус вписанной в него окружности равен 4. Найдите площадь этого треугольника.
Периметр треугольника равен 50, одна из сторон равна 20,
а радиус вписанной в него окружности равен 4. Найдите площадь этого треугольника.
По третьему свойству вписанной окружности, радиус вписанной окружности равен:
r=S/p, где S - площадь треугольника, а p - полупериметр.
p=50/2=25
S=r*p=4*25=100
Ответ: 100
Поделитесь решением
Присоединяйтесь к нам...
 Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 7:6, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 48.
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 7:6, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 48.
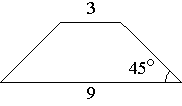 В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
 В треугольнике ABC с тупым углом ACB проведены высоты AA1 и BB1. Докажите, что треугольники A1CB1 и ACB подобны.
В треугольнике ABC с тупым углом ACB проведены высоты AA1 и BB1. Докажите, что треугольники A1CB1 и ACB подобны.
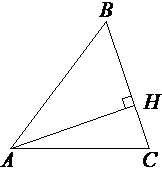 В остроугольном треугольнике ABC высота AH равна 20√
В остроугольном треугольнике ABC высота AH равна 20√
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABC к площади четырёхугольника KPCM.
Комментарии:
(2024-04-15 22:12:16) : Периметр треугольника равен 18, одна из сторон равна 7, а радиус вписанной в него окружности равен 3. Найдите площадь этого треугольника.
(2024-04-15 22:10:49) амина: Периметр треугольника равен 18, одна из сторон равна 7, а радиус вписанной в него окружности равен 3. Найдите площадь этого треугольника.