Радиус окружности, описанной около квадрата, равен 14√
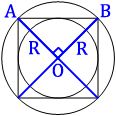Проведем диаметры
описанной окружности, как показано на первом рисунке.
Очевидно, что
квадрат разделился на 4 равных треугольника, углы, которые опираются на центр окружности (О), равны 360°/4=90°, т.е. эти треугольники
прямоугольные.
Тогда, по теореме Пифагора:
AB2=R2+R2
AB2=2R2
AB2=2(14√
AB2=2*142*2
AB2=142*22=(14*2)2=282
AB=28
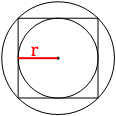Проведем радиус
вписанной окружности, как на втором рисунке.
Очевидно, что:
r=AB/2=28/2=14
Ответ: 14
Поделитесь решением
Присоединяйтесь к нам...
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 7:6, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 48.
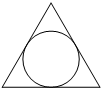Радиус окружности, вписанной в равносторонний треугольник, равен 2√
Найдите площадь треугольника, изображённого на рисунке.
В треугольнике ABC с тупым углом ACB проведены высоты AA1 и BB1. Докажите, что треугольники A1CB1 и ACB подобны.
Какие из следующих утверждений верны?
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Диагонали ромба равны.
3) Тангенс любого острого угла меньше единицы.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: