Четырёхугольник ABCD описан около окружности, AB=7, BC=10, CD=14. Найдите AD.
Вариант №1 (Предложил пользователь Людмила)
По второму свойству вписанной в четырехугольник окружности:
AB+CD=BC+AD
7+14=10+AD
AD=7+14-10=11
Ответ: 11
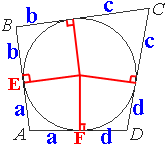AB и AD - это
касательные к окружности.Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) У равностороннего треугольника есть центр симметрии.
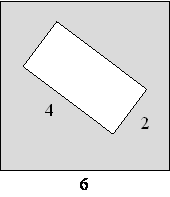Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Радиус вписанной в квадрат окружности равен 24√2. Найдите радиус окружности, описанной около этого квадрата.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=5, а расстояние от точки K до стороны AB равно 5.
В треугольнике ABC сторона AB=32, AC=64, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-05-14 20:24:54) Администратор: Людмила, спасибо большое за Ваше решение. Опубликовано от Вашего имени.
(2017-05-13 18:58:46) Людмила: Можно использовать теорему о том, что окружность можно вписать в четырехугольник тогда и только тогда, когда суммы его противоположных сторон равны. AB+CD=BC+AD, 7+14=10+AD