
 Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 10. Найдите BC, если AC=16.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 10. Найдите BC, если AC=16.
По
теореме об описанной окружности, центр описанной окружности лежит на точке пересечения
серединных перпендикуляров сторон треугольника.
У
прямоугольного треугольника центр окрудности лежит на середине гипотенузы, так же как и в треугольнике нашей задачи, следовательно данный треугольник
прямоугольный.
Следовательно, можно применить
теорему Пифагора:
AB2=BC2+AC2
AB - диаметр окружности, так как проходит через центр.
Тогда AB=2*R=2*10=20.
202=BC2+162
400=BC2+256
BC2=400-256=144
BC=12
Ответ: 12
Поделитесь решением
Присоединяйтесь к нам...
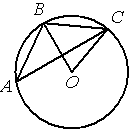 Точка О – центр окружности, /BAC=20° (см. рисунок). Найдите величину угла BOC (в градусах).
Точка О – центр окружности, /BAC=20° (см. рисунок). Найдите величину угла BOC (в градусах).
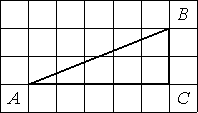 Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
 В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 13 и 7. Найдите площадь параллелограмма ABCD.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 13 и 7. Найдите площадь параллелограмма ABCD.
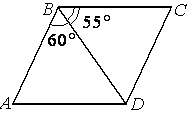 Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
60° и 55°. Найдите меньший угол параллелограмма.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
60° и 55°. Найдите меньший угол параллелограмма.
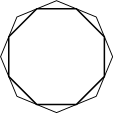 Дан правильный восьмиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный восьмиугольник.
Дан правильный восьмиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный восьмиугольник.
Комментарии: