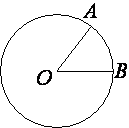
На окружности с центром в точке O отмечены точки A и B так, что ∠AOB=66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги AB.
∠AOB является центральным, поэтому градусная мера дуги, на которую он опирается тоже равна 66°.
Так как градусная мера всей окружности составляет 360°, то градусная мера большей дуги равна:
360°-66°=294°
Теперь систавим пропорцию:
Для 66° - длина дуги 99
Для 294° - длина дуги x
66/294=99/x
x=294*99/66=294*1,5=441
Ответ: 441
Поделитесь решением
Присоединяйтесь к нам...
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=12, CM=18. Найдите AO.
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=20, DK=15, BC=12. Найдите AD.
Радиус вписанной в квадрат окружности равен 2√2. Найдите диагональ этого квадрата.
Укажите номера верных утверждений.
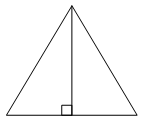1) Центры вписанной и описанной окружностей равностороннего треугольника совпадают.
2) Существует квадрат, который не является ромбом.
3) Сумма углов остроугольного треугольника равна 180°.
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=97 и BC=BM. Найдите AH.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: